Normalization

Normalize

Mapping extended entity-relationship (EER) diagrams to relations always results in a normalized database, yet we must still learn about normalization. For one, the databases we build will likely outlive the EER diagrams from whence they came, so we should know how to continue to evolve them in a normalized fashion.

Additionally, we never know what we might find when we inherit a database: it may be beautifully normalized and appear designed by experts, or it may not be normalized and look like idiots built it. Either way, we have to know how to navigate the database and understand that there may be situations in which normalization is relaxed in the face of other competing requirements, such as performance.

What it's all About

Consider the RegularUser relation below with Email, Interest, SinceAge, Birth Year, Current City, and Salary columns.

This relation has some dependencies amongst the columns, so-called functional dependencies. We will examine three such dependencies in this relation:

1. The email address for a given user determines their birth year, current city, and salary.
2. The combination of email address and interest determines the age since that user has held that interest.
3. The birth year of a given user determines their salary.

Does this relation's current structure make it easy to enforce these dependencies? How might we normalize this relation - or decompose it into smaller relations - without losing information or violating the dependencies?

The Rules

Here are the rules we must obey when normalizing a relation:

1. No redundancy of facts
2. No cluttering of facts
3. We must preserve information
4. We must preserve functional dependencies

Not a Relation

We might lay out the regular user data in the following nonrelational, non first normal form data structure:

In this data structure, each user row contains single-valued attributes for email, birth year, current city, and salary. Additionally, each user may have multiple values for Interest and SinceAge. For example, user one has been interested in music since age ten, reading since age five, and tennis since age fourteen.

If we recall the definition of a relation, we might remember that we pull values for attributes from sets of atomic values. Certainly, (Music, Reading, Tennis) and (10, 5, 14) are not atomic values. How might we turn this non first normal data structure into a relation?

An obvious solution is to repeat information. For example, instead of having one row with two three-valued attributes for user one, we can create three rows. We have to repeat the user's email, birth year, current city, and salary three times - once for each row - but we do end up with a relation.

Relation with Problems

Let's convert the non first normal form data structure into a relation. As we said, we will add a row per value in the multi-valued attributes and repeat the single-valued attributes in each row. Even though we repeat information - for example, user one's Email, Birth Year, Current City, and Salary three times - we now only have one Interest/SinceAge pair per row.

This data structure is now a relation, but it has many problems. Let's see what trouble we have created for ourselves.

Relation with Problems: Redundancy

The first problem this relation has is redundancy. Because we repeated user one's information - Email, Birth Year, Current City, and Salary - to avoid the multi-value problem, we now have redundant information, and redundancy potentially leads to inconsistency.

Suppose user one moves from Seattle to Atlanta. Furthermore, suppose that we update the Current City value for user one in row one from Seattle to Atlanta, but we somehow miss applying that update in rows two or three. Subsequent database users will be unable to discern user one's current city. This inconsistency, facilitated by redundancy, renders the database useless for queries about a user's current city.

Relation with Problems: Insertion Anomaly

Let's say we insert a new user, user nine, into the database with their corresponding birth year, current city, and salary information. If user nine doesn't have any interests, then we have to insert NULL values for Interest and SinceAge.

Let's say we want to insert the information in the database that people born in 1970 make 42000. If we don't already have a user born in 1970 in RegularUser, we must insert a new row that has 1970 for Birth Year, 42000 for Salary, and NULL for every other attribute.

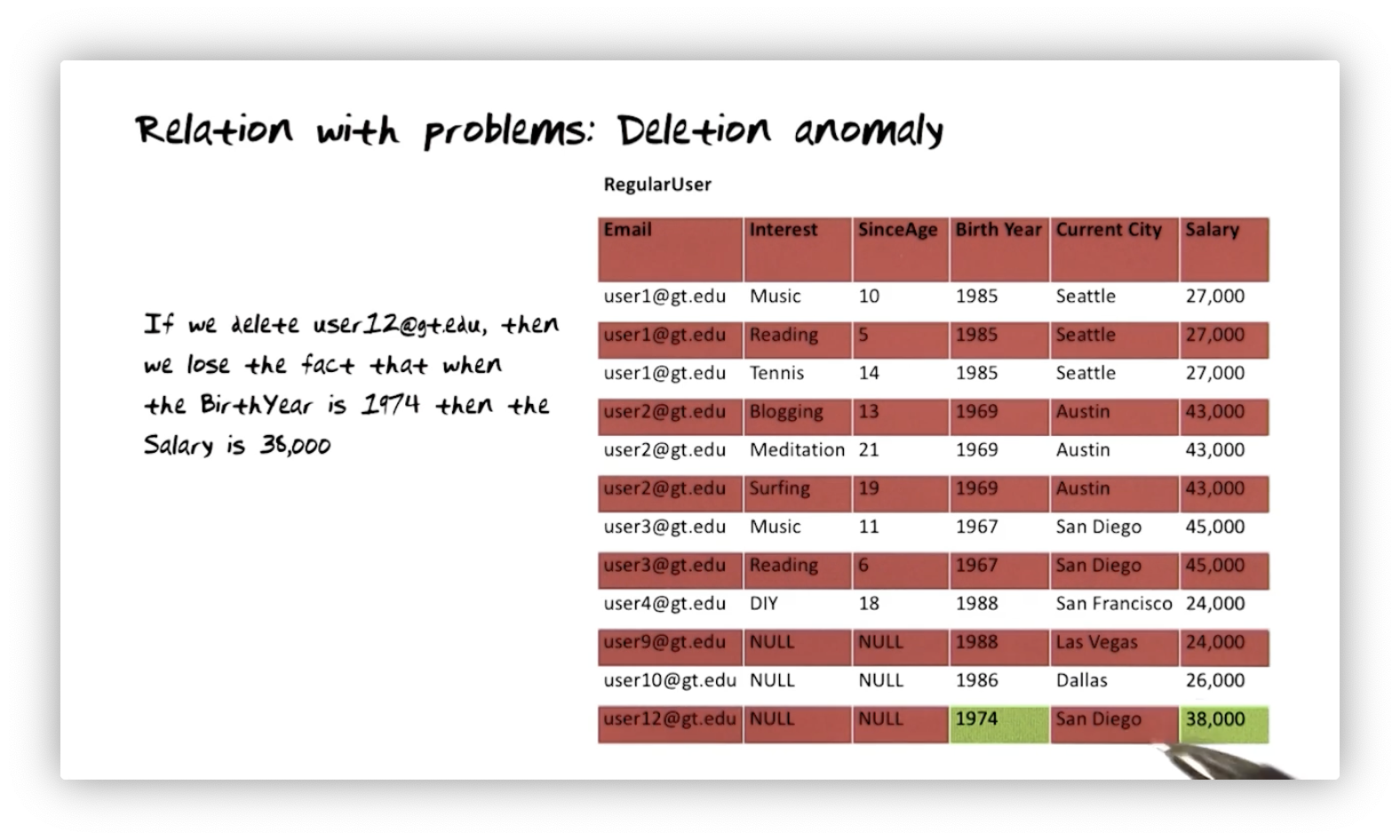
Relation with Problems: Deletion Anomaly

Here we want to delete user twelve from the database. Unfortunately, since this user is the only regular user born in 1974, by deleting this row, we also lose the information that people born in 1974 make 38000.

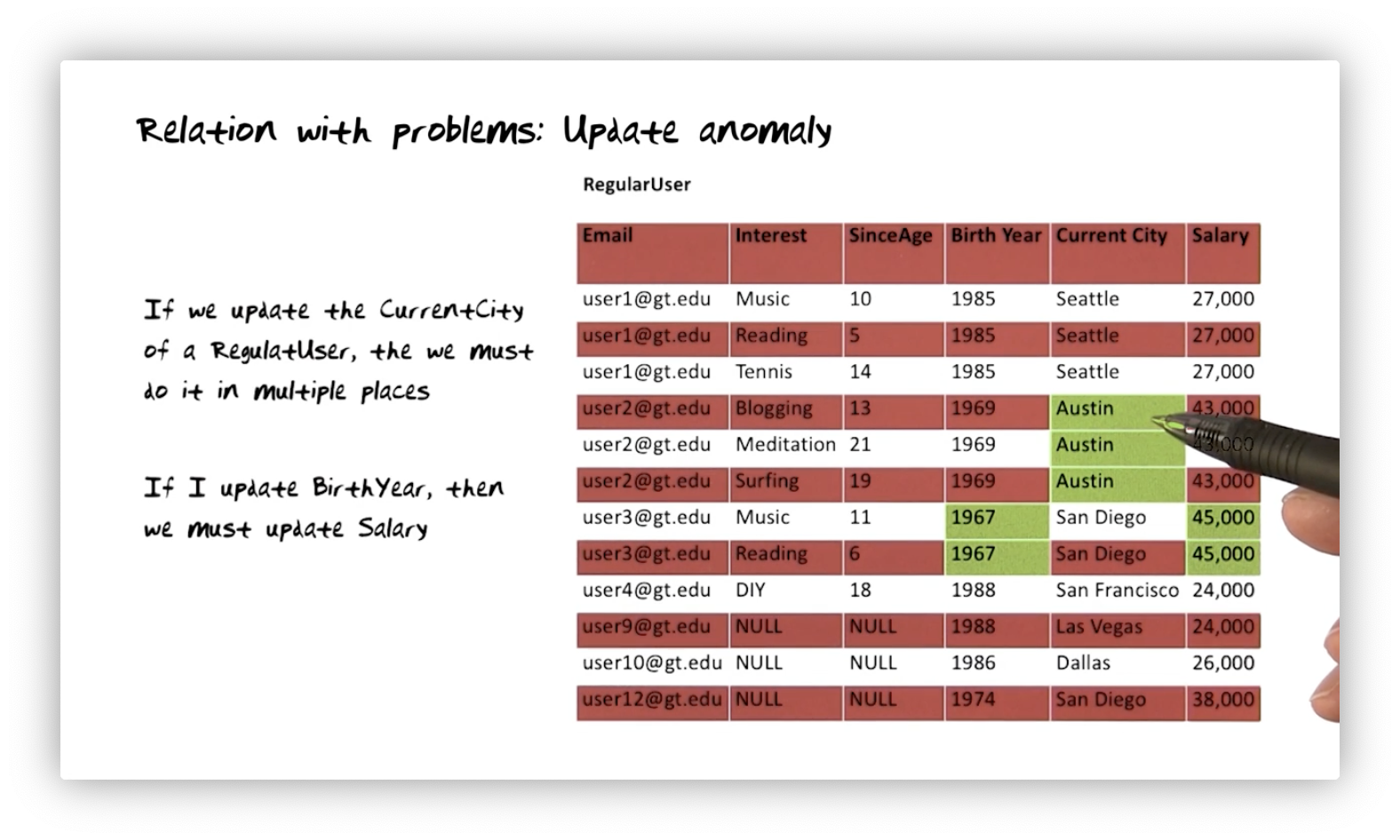
Relation with Problems: Update Anomaly

If we want to update the current city for user two, we must update it for every row containing user two's information. Similarly, if we want to update the salaries made by people born in 1967, we must touch every row with 1967 as the Birth Year.

Information Loss

Decomposing this table into multiple tables enables us to enforce the functional dependencies we discussed without issue. A correct decomposition process retains all the information from the initial table in the resulting tables.

Consider the following decomposition of the RegularUser table into two tables. We project RegularUser onto Email, Interest, SinceAge, Birth Year, and Current City to produce table A on the right. Similarly, we project RegularUser on Current City and Salary to create table B on the left.

Even though structuring the data in one relation presented problems, we still want a mechanism to reconstitute that view. When we decompose a table, we must share at least one attribute between the two resulting tables. In this case, A and B share the Current City attribute, and if we join them on Current City, we can recreate RegularUser.

Unfortunately, this particular decomposition has an issue. Table B has two tuples where the value of Current City is San Diego. When we join B and A, we will get two tuples for user three and user twelve, one for each tuple in B referencing San Diego. Joining the two decomposed relations together creates two additional rows absent from RegularUser.

We call this phenomenon information loss. Even though we are getting more information in this situation, not less, we have lost our ability to distinguish between what is real and what is false. We are now unable to determine the salary of those two users accurately.

Dependency Loss

When all the information is together in the original table, it is possible to enforce the functional dependencies of our system. However, we may lose that ability when decomposing a table into multiple tables. Remember the decomposition from earlier.

We have two examples of such dependency loss here. We have one functional dependency stating that Email must dictate Salary. Similarly, we said Birth Year must determine Salary. Since neither of these pairs of attributes exists in the same table, we cannot enforce the dependency between them in a table.

Perfect

Let's decompose RegularUser into three relations.

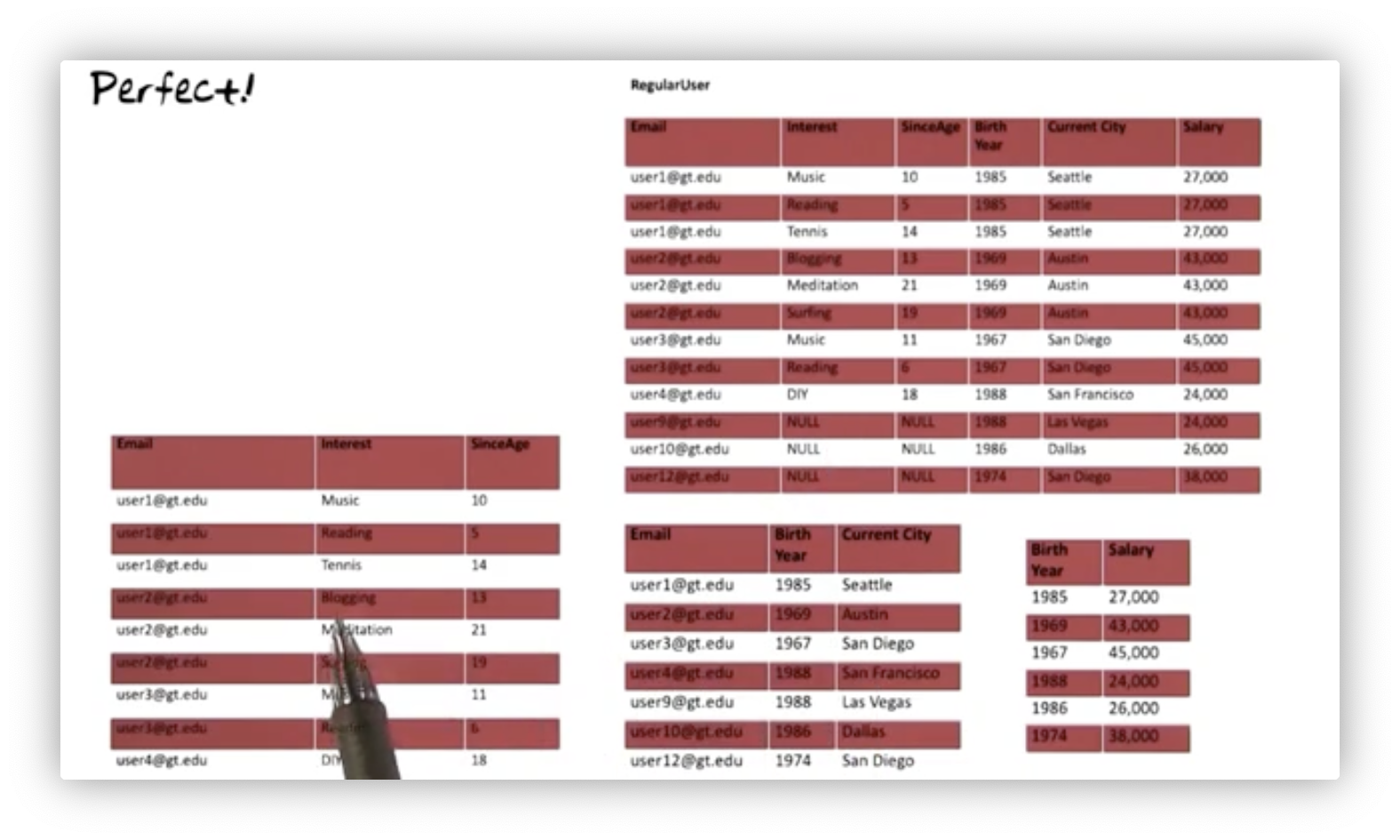
The original RegularUser table had many redundancies, e.g., user one's information repeated three times, one for each interest. This decomposition eliminates all redundancies, making it impossible for us to end up with an inconsistent database.

We've avoided insertion anomalies because the facts represented by the functional dependencies exist in different tables. Consequently, we won't see any deletion anomalies because we can delete one fact without inadvertently deleting other facts for a particular regular user. Additionally, there won't be any update anomalies because there is no redundant information.

This decomposition does not introduce any information loss. Joining these decomposed tables produces exactly the information in the original RegularUser table: no less, no more. We also have no dependency loss. We have a separate relation for each dependency:

• Email and Interest determine SinceAge in the table on the left
• Email determines Birth Year and Current City in the middle table
• Birth Year determines Current Salary in table three

The big question is: how do we get here? In other words, starting with RegularUser, how do we arrive at this particular decomposition out of the many possibilities?

Functional Dependencies

Let's start by defining functional dependencies. If $X$ and $Y$ are sets of attributes in relation $R$, then we say that $Y$ is functionally dependent on $X$ iff for each $x$ in $R.X$, there is precisely one $y$ in $R.Y$. Consider the following relations.

On the left, we see a relation with Email, Birth Year, and Current City attributes. Current City is functionally dependent on Email if, for each value of Email, there is precisely one value of Current City. Similarly, Birth Year is functionally dependent on Email if, for each value of Email, there is precisely one value of Current City. Since each Email only appears once in that table, Current City and Birth Year must be functionally dependent on it.

On the right, we see a relation with Email, Interest, and SinceAge attributes. In this example, we express that SinceAge is functionally dependent on Email and Interest. This functional dependency is present if, for every pair of Email and Interest, there is precisely one value for SinceAge. Looking at this table, we see no repeated pairs of Email and Interest, with each pair mapping to a single value of SinceAge.

Now that we've seen how to identify a functional dependency, how do we enforce one?

Full Functional Dependencies

Let's look at another definition. Let $X$ and $Y$ be sets of attributes in $R$. Then, $Y$ is fully functionally dependent on $X$ in $R$ iff $Y$ is functionally dependent on $X$ and $Y$ is not functionally dependent on any proper subset of $X$. Consider the following relations.

In the relation on the left, we want to express that only Email and Interest together determine SinceAge; in other words, neither Email nor Interest alone is sufficient. If we look at all tuples associated with user one, we see a different value of SinceAge in each. Similarly, if we look at all tuples associated with the interest "Music", we see different SinceAge values. Therefore, we can say SinceAge is fully functionally dependent on Interest and Email.

In the relation on the right, we want to express that Email and Interest determine Current City, Birth Year, and Salary. Let's look at Current City. This attribute is not fully functionally dependent on Email and Interest because it's dependent on Email alone. As we can see from the table, every value of Email maps to a single Current City. We don't need Email and Interest together to determine Current City (or Birth Year or Salary, for that matter).

Functional Dependencies and Keys

We use keys to enforce functional dependencies. If we want to enforce the functional dependency that $X$ determines $Y$, we need to make $X$ the key in that relation. Let's look at some examples.

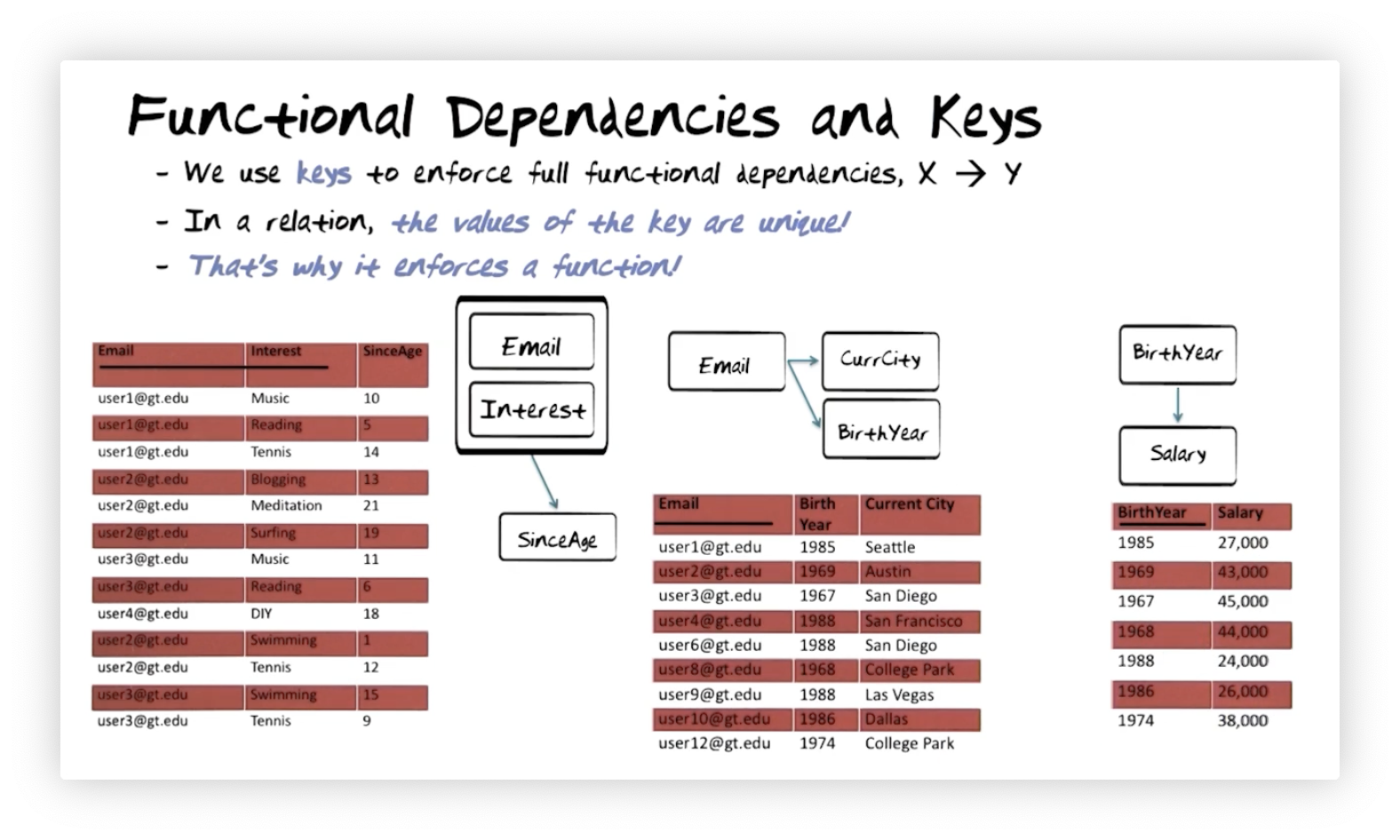
On the left, we can see that making Email and Interest the key enforces the functional dependency that Email and Interest determine SinceAge. Why? Because by making that pair of attributes the key, we require that no duplicate values are present. Since there are no duplicate values, a particular Email and Interest pair will determine exactly one SinceAge.

For the relation in the middle, we need to enforce the dependency that Email determines Current City and Birth Year. Again, we make Email the key, so the values for that attribute will be unique. Thus, each Email will map to a single Birth Year and Current City.

On the right, we want to enforce the functional dependency that Birth Year determines Salary. We can follow the pattern from the other two examples and make Birth Year the key. Again, the uniqueness constraint on key values means that a particular Birth Year will always point to exactly one Salary.

These relationships are functions; in other words, given an input $X$, these dependencies always produce one value of $Y$. There's a function from the pair of Email and Interest to SinceAge, from Email to Birth Year, from Email to Current City, and from Birth Year to Salary.

Overview of Normal Forms

We will now introduce four normal forms, which will help us recognize how well a relation is laid out. We refer to data structures that do not qualify as any of these normal forms as non first normal forms (NF2). Non first normal form data structures are not relations as we have defined them thus far.

Some subset of all data structures qualifies as first normal form (1NF) relations. A subset of these relations is second normal form (2NF) relations. Of the second normal form relations, there is a subset called the third normal form (3NF) relations. Finally, within the third normal form relations are a set of Boyce–Codd normal form (BCNF) relations. These forms are what we aim for when we are attempting to normalize a relation.

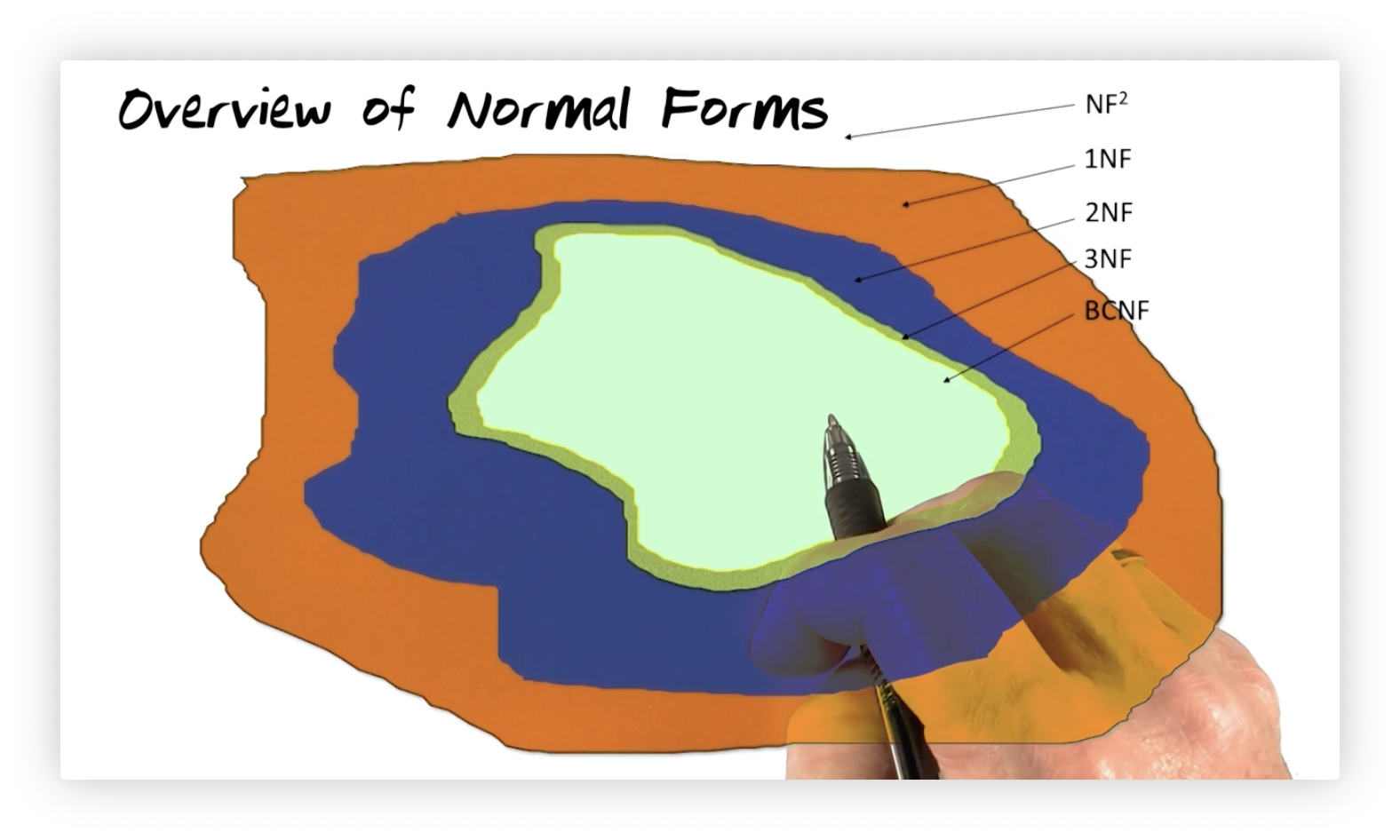
If we look at the diagram above, we see that there are certainly first normal form relations that are not in second normal form and also second normal form relations that are not in third normal form. Notice, however, the overlap between the third normal forms and Boyce-Codd normal forms. While it is theoretically possible that you have a relation in third normal form that is outside of Boyce-Codd normal form, we rarely encounter this scenario in practice.

Normal Forms: Definitions

A relation, $R$, is said to be in first normal form if all domain values are atomic. Remember that we defined a relation as a data structure whose domain values are drawn from sets of atomic values. All relations are automatically born in first normal form. $R$ is in second normal form if it is in first normal form and every non key attribute is fully dependent on the key. $R$ is in third normal form if it is in second normal form and every non key attribute is non-transitively dependent on the key. Finally, $R$ is in Boyce-Codd normal form if it is in third normal form and every determinant is a candidate key. A determinant is a set of attributes in a relation on which some other attribute is fully functionally dependent.

Kent and Diehr Quote

The Kent and Diehr quote, which resembles the sworn testimony oath in the United States, is:

All attributes must depend on the key (1NF), the whole key (2NF), and nothing but the key (3NF), so help me Codd.

1NF to BCNF Flowchart

Recall again the example relation we have been studying. This relation has Email, Interest, Current City, Birth Year, Salary, and SinceAge, and the following functional dependencies:

• Email and Interest together determine SinceAge.
• Email determines Current City, Birth Year, and Salary.
• Birth Year also determines Salary.

The diagram below depicts the decomposition of a single first normal form relation into three Boyce-Codd normal form relations, with an intermediate second normal form relation. Let's walk through the decomposition.

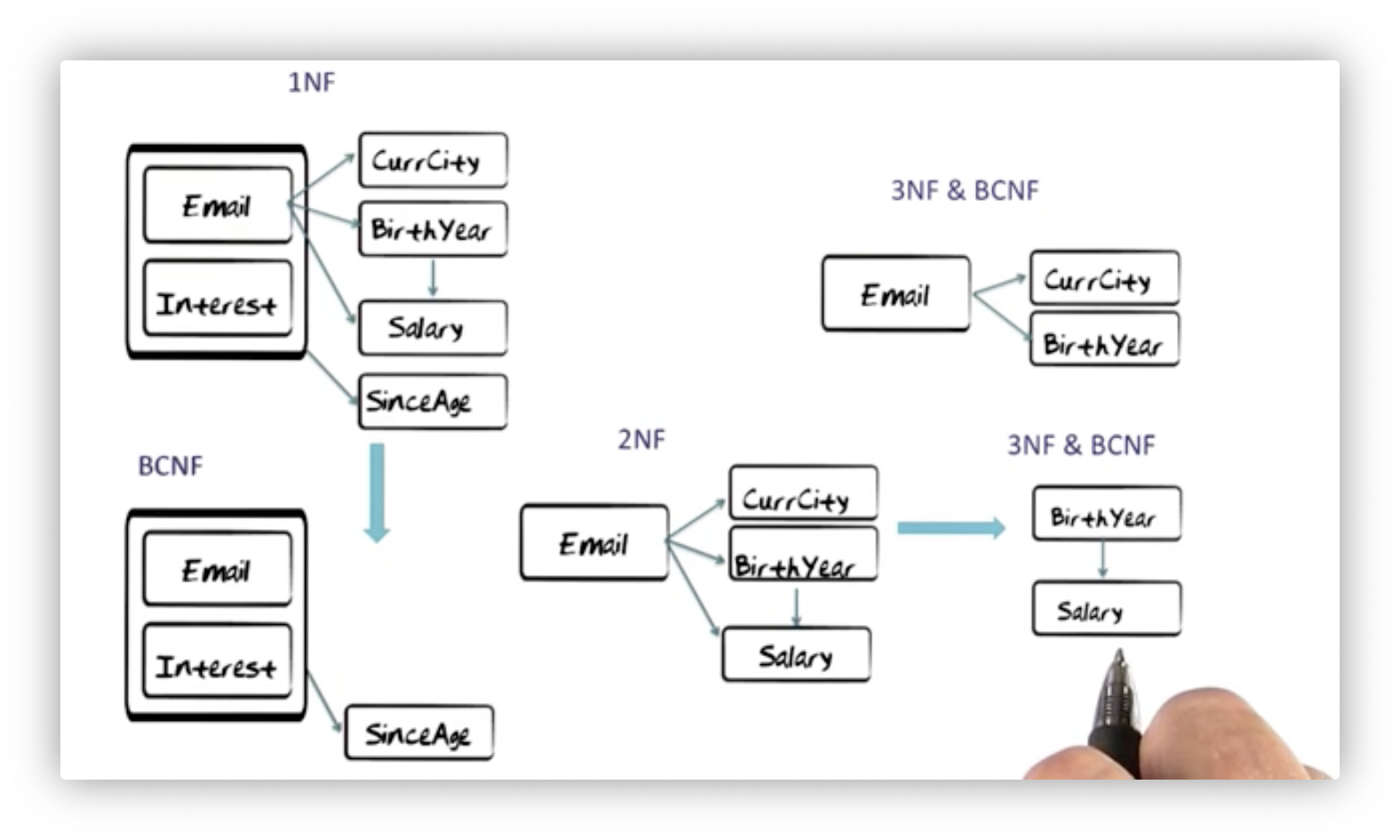
First, we extract the functional dependency between Email/Interest and SinceAge, creating a relation containing those three attributes. This relation must be in Boyce-Codd normal form because the only determinant is the Email/Interest pair, which has to be a candidate key to enforce that functional dependency.

Extracting this relation leaves us with a relation containing Email, Current City, Birth Year, and Salary attributes. What normal form is this relation in? It must at least be in second normal form because all of these attributes fully depend on the key, Email. Unfortunately, there are transitive dependencies: Email determines Birth Year, which in turn determines Salary, resulting in the functional dependency from Email to Salary, so it is not in third normal form.

Let's extract two relations: one containing Email, Current City, and Birth Year attributes, and another containing Birth Year and Salary attributes. Neither relation contains transitive dependencies outside of the key, so they must be in third normal form. The first relation is also in Boyce-Codd normal form because its only determinant is Email, which must be the key to enforce the second functional dependency. The second relation is also in Boyce-Codd normal form because its only determinant is Birth Year, which must be the key to enforce the third functional dependency.

How to Compute with Functional Dependencies: Armstrong's rules

We use Armstrong's rules, named after William Armstrong, to ensure that we do not lose information and that we preserve functional dependencies when we decompose relations.

The rule of reflexivity states that if $Y$ is a subset of $X$, then $X$ functionally determines $Y$. For example, Email, Interest functionally determines Interest.

The rule of augmentation states that if $X$ functionally determines $Y$, then $WX$ functionally determines $WY$. For example, if Email determines Birth Year, then Email, Interest determines Birth Year, Interest.

The rule of transitivity states that if $X$ determines $Y$, and $Y$ determines $Z$, then $X$ determines $Z$. For example, if Email determines Birth Year, and Birth Year determines Salary, then Email determines Salary by transitivity.

How to Guarantee Lossless Joins?

We must ensure that the join field is a key in at least one of the resulting relations to guarantee lossless joins when we decompose a relation. Consider the decomposition below. The join field is obviously Email. Since Email is a key in either of these two relations, we will not lose information when joining these tables. Therefore, this decomposition is lossless.

When we join these two relations again on Email, we are guaranteed not to create additional tuples that were not present in the original relation.

How to Guarantee Preservation of Functional Dependencies?

We can guarantee the preservation of functional dependencies by ensuring that the meaning implied by the remaining functional dependencies is the same as that implied by the original set.

An original functional dependency, we had stated that Email must determine Salary. In our final set of relations, we see that only Birth Year explicitly determines Salary. However, we also see that Email determines Birth Year, and we know by transitivity that Email must determine Salary. Therefore, the meaning implied by the final set of functional dependencies is the same as the original set, even if this particular dependency is no longer explicit.

Email Interest

Let's return to the decomposition we performed previously.

First, we decomposed this relation into two relations. For this to be a lossless decomposition, the join field - in this case, Email - must be a key in at least one of the two relations. We know that Email must be the key to enforce the dependencies. Is the decomposition dependency preserving? Yes again. We haven't decomposed out any transitive dependencies, so all dependencies remain explicit.

When we further decompose the second normal form relation, let's ask the same two questions again. Is the decomposition lossless? The join attribute here is Birth Year, which is definitely the key in one relation. Therefore: the join is lossless. The decomposition is also dependency preserving. Email determines Birth Year, which determines Salary. The functional dependency of Salary on Email is implied by transitivity, which is the only dependency that is not explicit.

3NF and BCNF

Boyce-Codd normal form relations are a proper subset of third normal form relations. It's possible to find relations that we can decompose only to third normal form - but not Boyce-Codd normal form - while being lossless and dependency preserving. This scenario only happens in cases where the relation has overlapping keys.

It Never Happens in Practice

It really never happens in practice that there is a third normal form relation that is not also in Boyce-Codd normal form. In his thirty-five years of professional work with databases, Professor Mark has never seen it.