Extended-Entity Relationship Model

Introduction

This course focuses heavily on data modeling, and we need data models to perform data modeling. The extended entity-relationship model is one data model that is particularly good at helping us fix and represent a perception of reality.

Entity Type and Entity Surrogates

The entity type is the first concept we encounter from the extended entity-relationship model. An entity type is a time-invariant person, concept organization, or object type about which we want to store information. We represent entity types with rectangles, as shown below with the User entity type.

Within one entity relationship diagram, all entity type names must be unique. In this system, for example, we could not have multiple entity types called User.

Our system may contain zero or more concrete instances of the entity types we define. For example, our system may have eight users, each modeled by the User entity type. Each user instance is a surrogate, an object in our system representing a user in the real world.

Single-valued Properties

We use property types to define attributes on entity types, and we represent property types using ellipses. Here we have a User entity type with Email and Password property types.

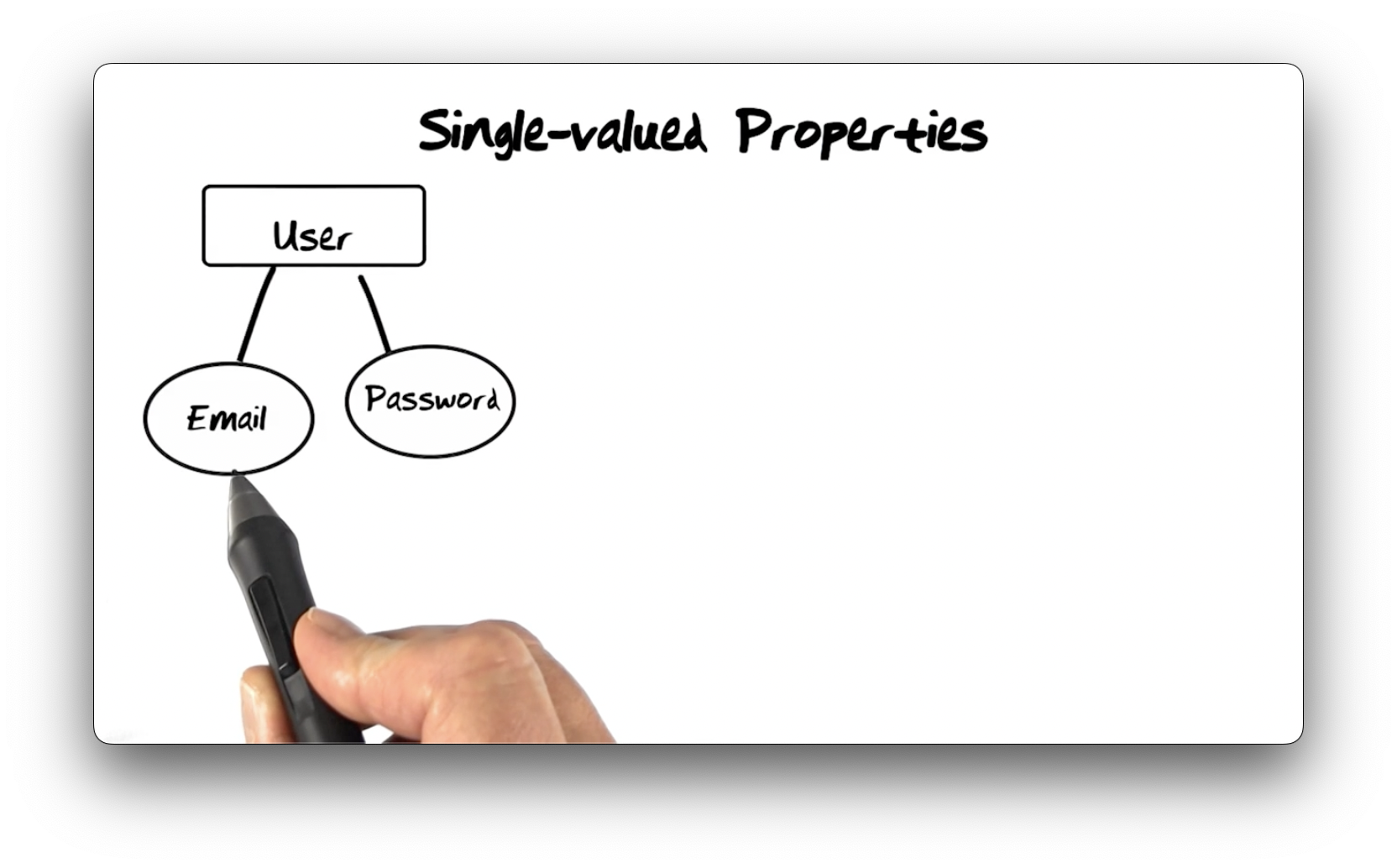
The ellipses above have only a single line, which indicates that the properties they enclose are single-value properties.

Let's look at some users in our system: the first user has the email "leo@gt.edu" and the password "qwerty"; the second user has the email "rocky@gt.edu" and the password "lydia10411", and; the last user has the email "jim@gt.edu" and the password of "fido123".

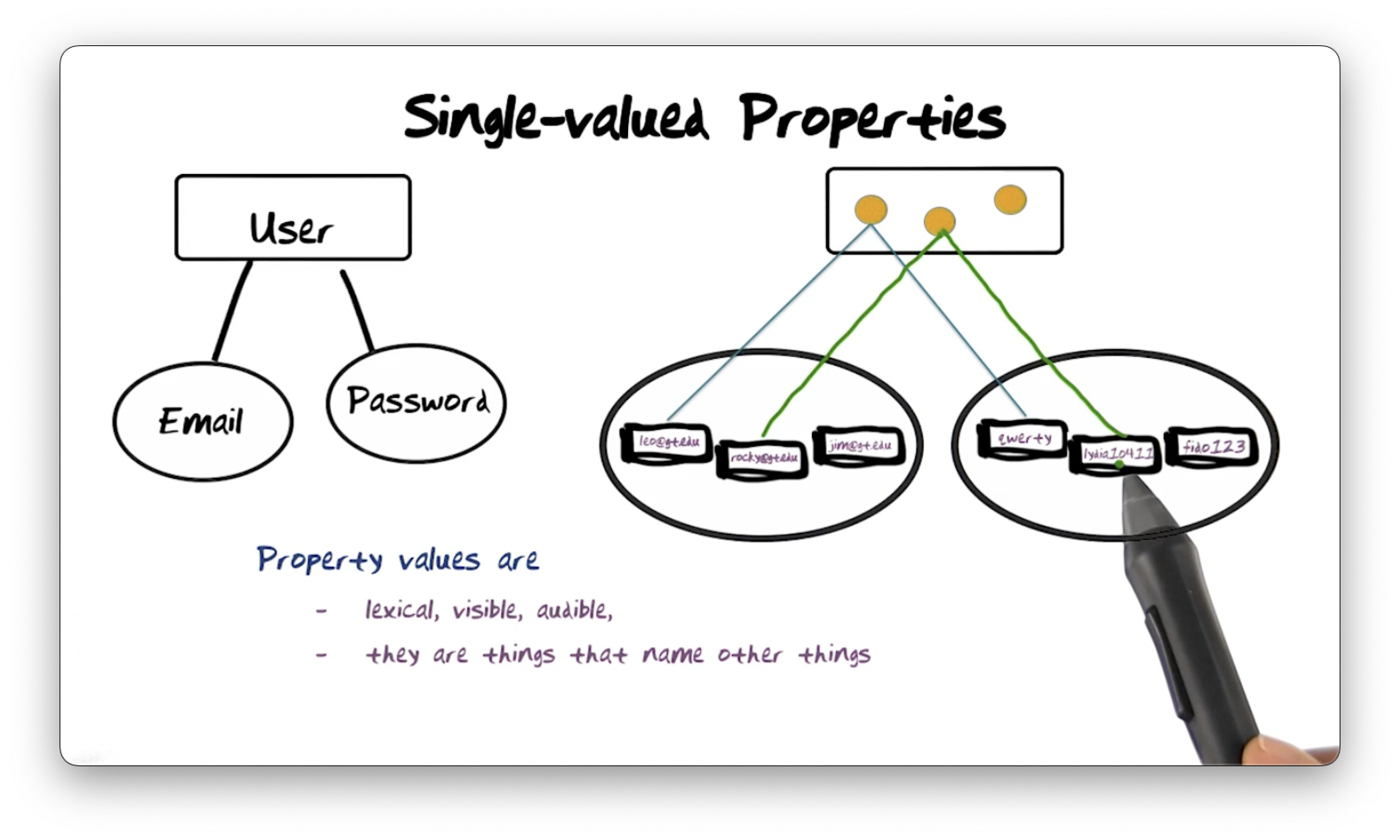
Property values can take many forms. They can be lexical (using letters), visible - like a picture of a user - or audible, such as a recording of a name.

Identifying Properties

An identifying property type is a property type whose value uniquely identifies the instance of the associated entity type. We represent these property types by underlining their name. In the diagram below, the Email property type identifies instances of the User entity type; consequently, no two users in the system can have the same email.

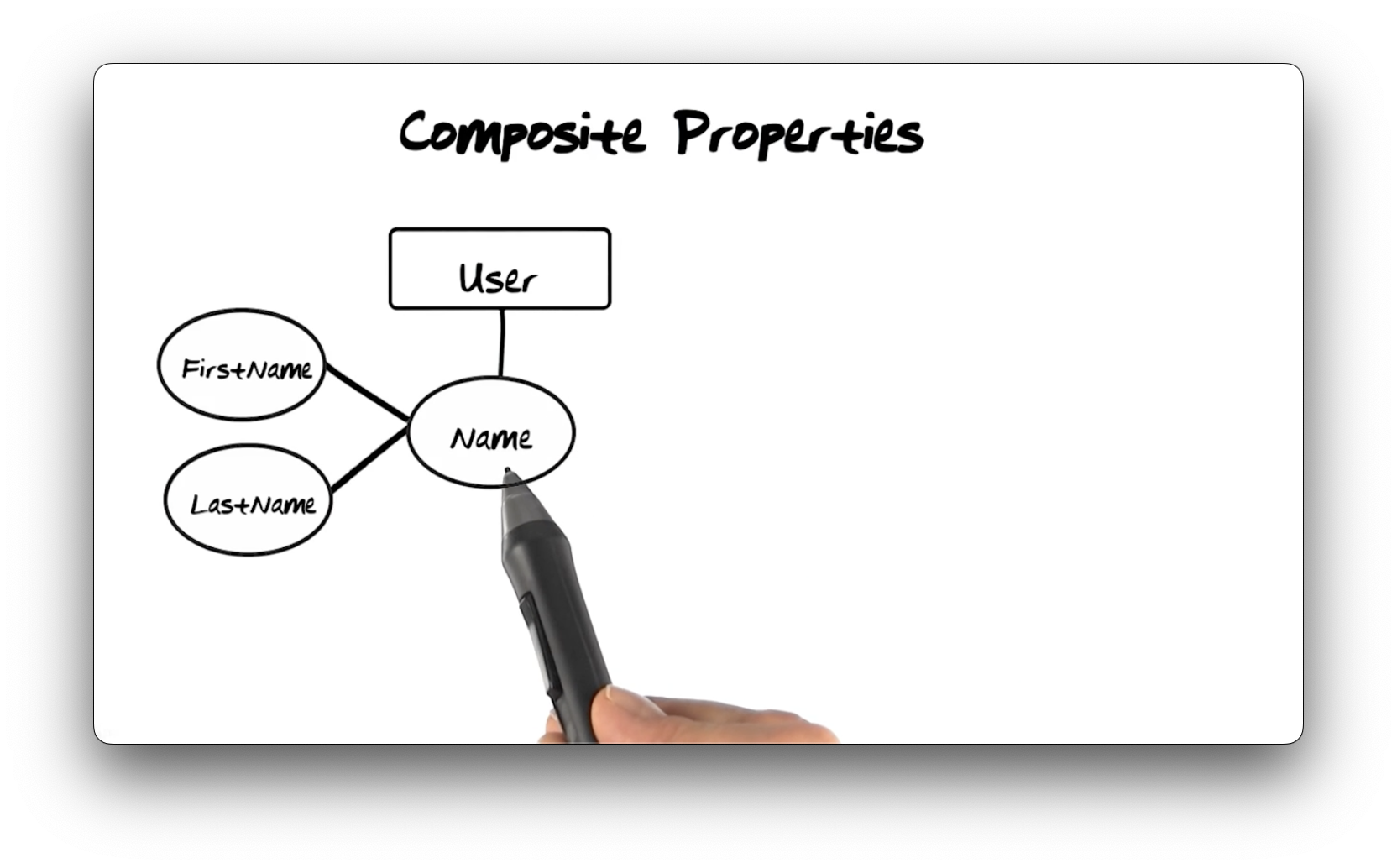
Composite Properties

We can combine two or more property types to create composite property types. In the following diagram, we have a User entity type with a Name property type composed of FirstName and LastName property types. In our system, for example, we may have a user instance whose name is "Jim Smith". Their first name is "Jim", and their last name is "Smith".

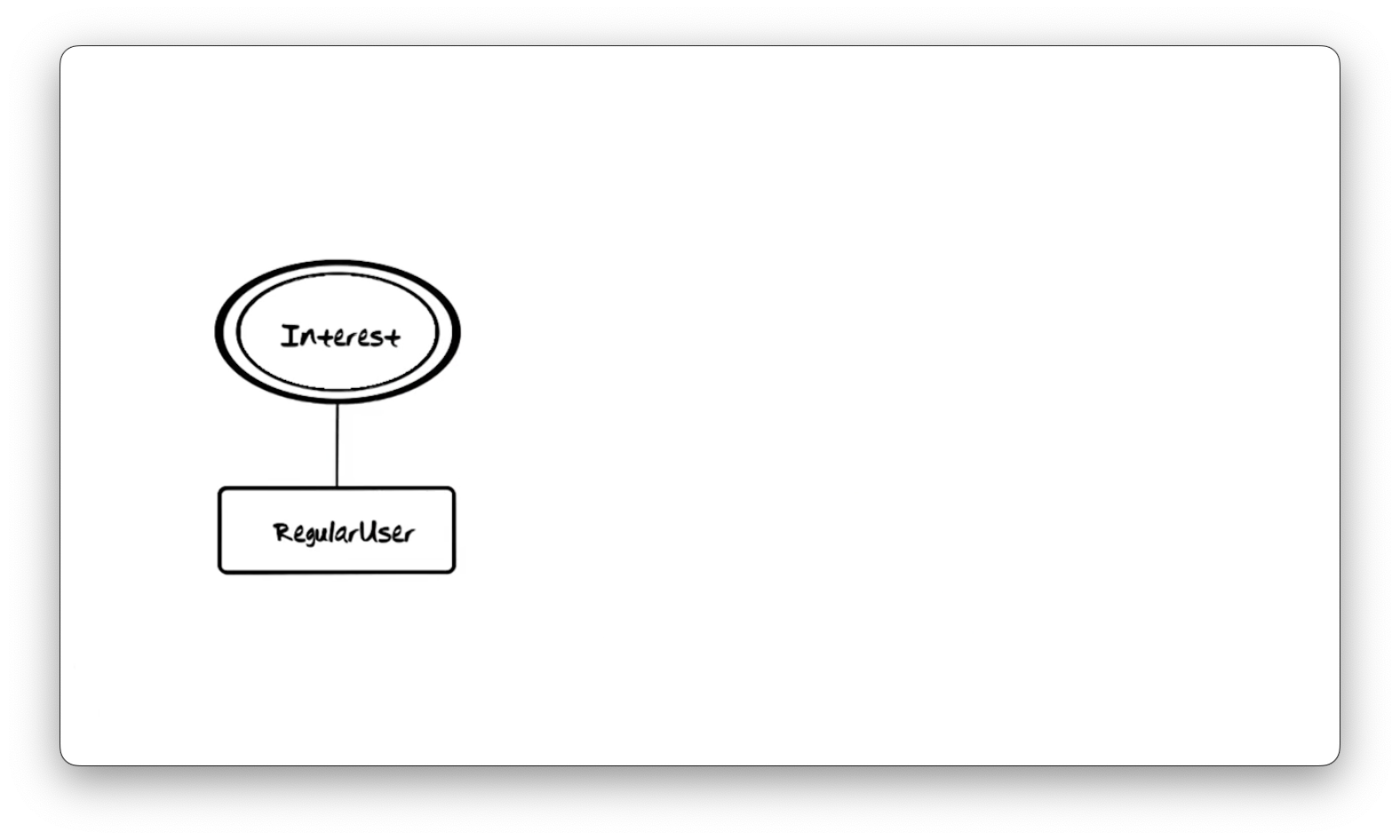
Multi-valued Properties

Multi-valued property types can have more than one value. We represent these property types with a double ellipsis. Here we have a RegularUser entity type with a multi-value property type called Interest. One instance of this entity type might have "chess", "reading", and "math" as interests, while another might have "chess" and "baseball" as interests.

1-1 Relationship Types

Relationship types describe relationships between entity types, which we represent using diamonds. Consider the following diagram, depicting a Current Marriage relationship type that connects the MaleUser and FemaleUser entity types.

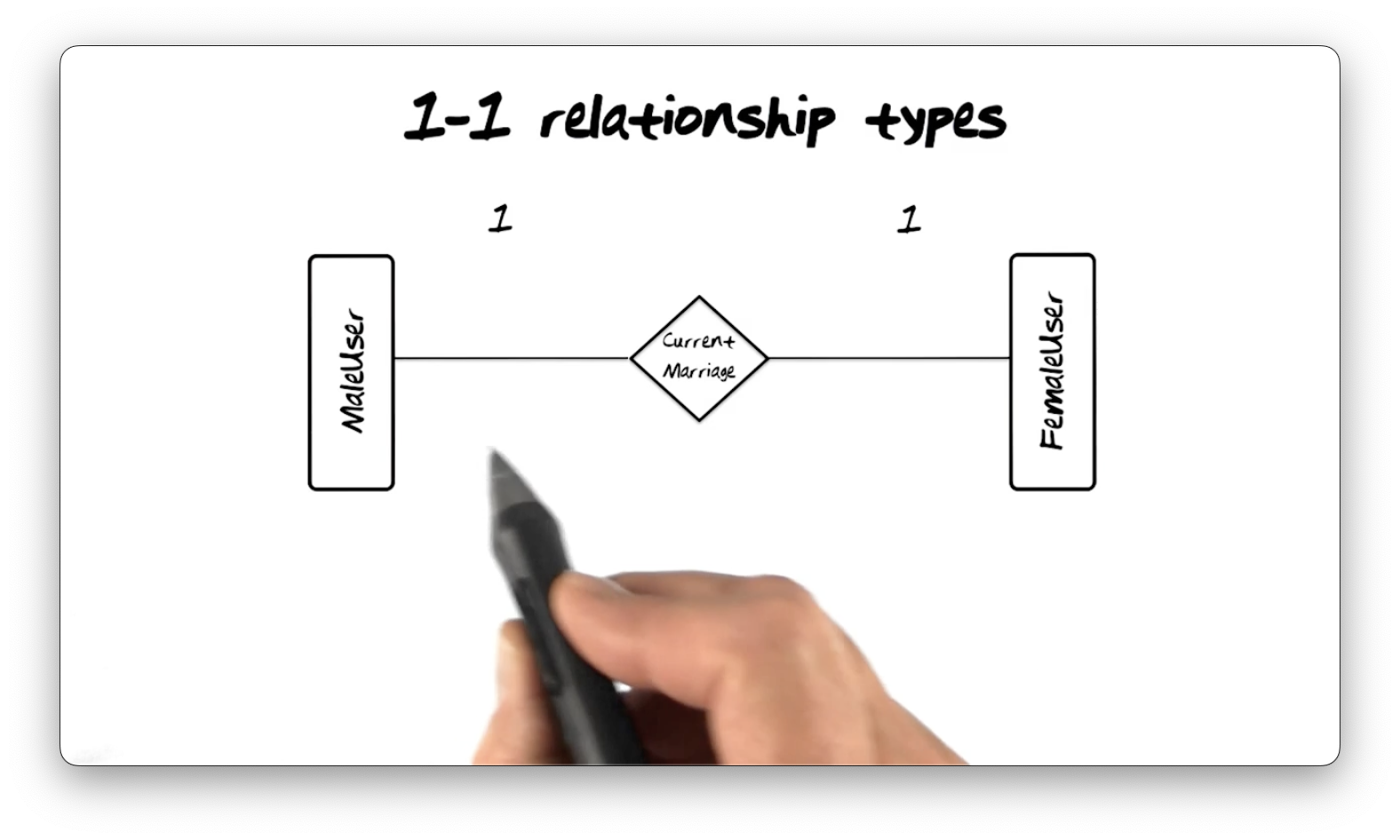
The numbers above the lines connecting the entity types to the relationship type express the cardinality of the relationship. Here, one MaleUser instance and one FemaleUser instance are present in the Current Marriage relationship type. This configuration is known as a 1-1 relationship type.

Not all instances of entity types for which a relationship type is present must participate in that relationship. For example, we can have single MaleUser and FemaleUser instances. As a result, the Current Marriage relationship type is a partial function. It's a function because it maps instances of one entity type to the other, but it's only a partial function because some instances do not map to anything, i.e., single users.

Relationship type names must be unique within the context of the connected entity types. For example, we cannot have two relationship types named Current Marriage that connect MaleUser and FemaleUser. We could have a Current Marriage relationship type between two other entities, but we could have a Friendship relationship type between MaleUser and FemaleUser.

1-Many Relationship Types

The next relationship type we examine is the 1-many relationship type, which connects one instance of one entity type to zero or more instances of another entity type. For example, consider the following relationship between the Employer entity type and the RegularUser entity type.

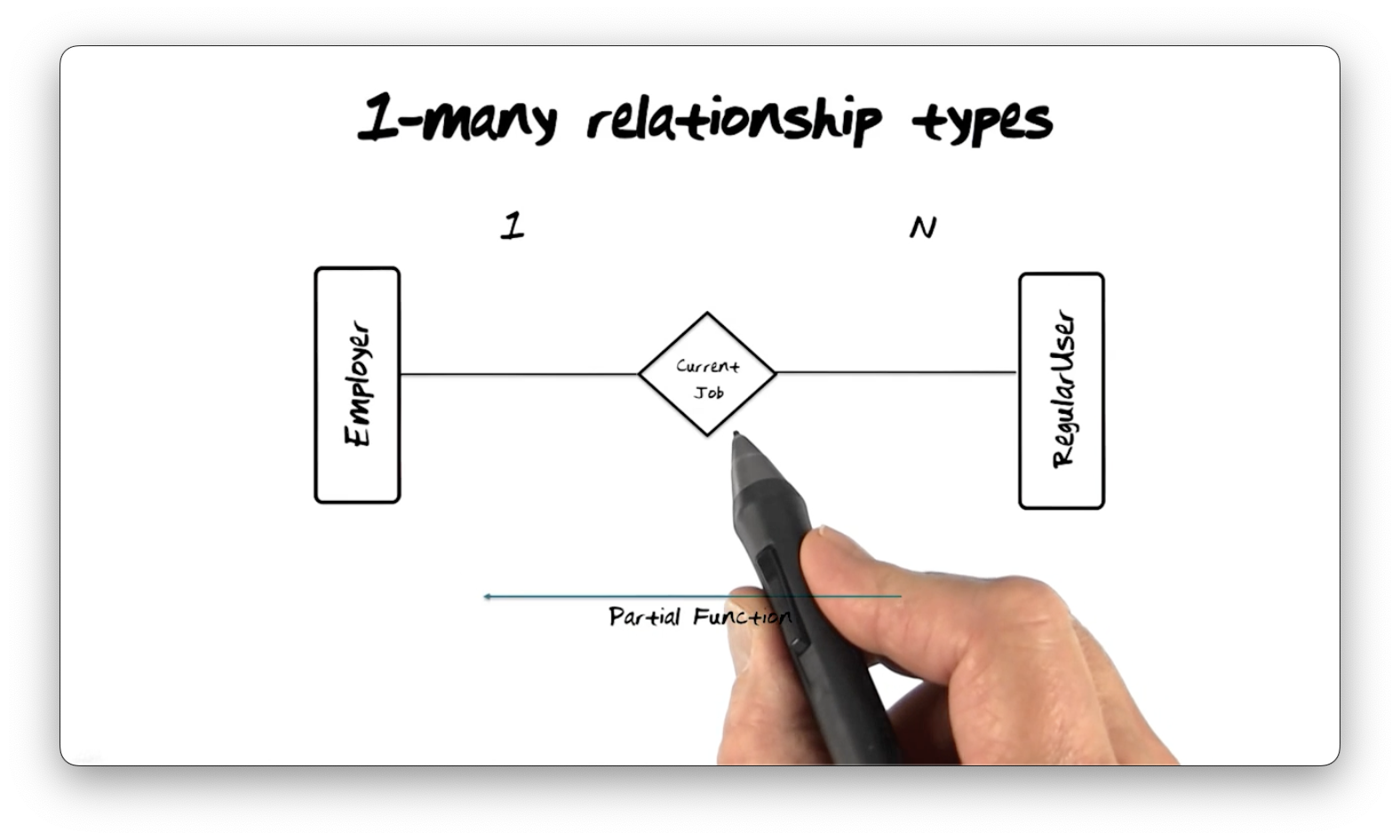
Each employer may employ zero, one, or many users. The 1-many relationship is also a partial function because it maps some subset of Employer instances to some subset of RegularUser instances. Not every employer has employees, and not every user is employed.

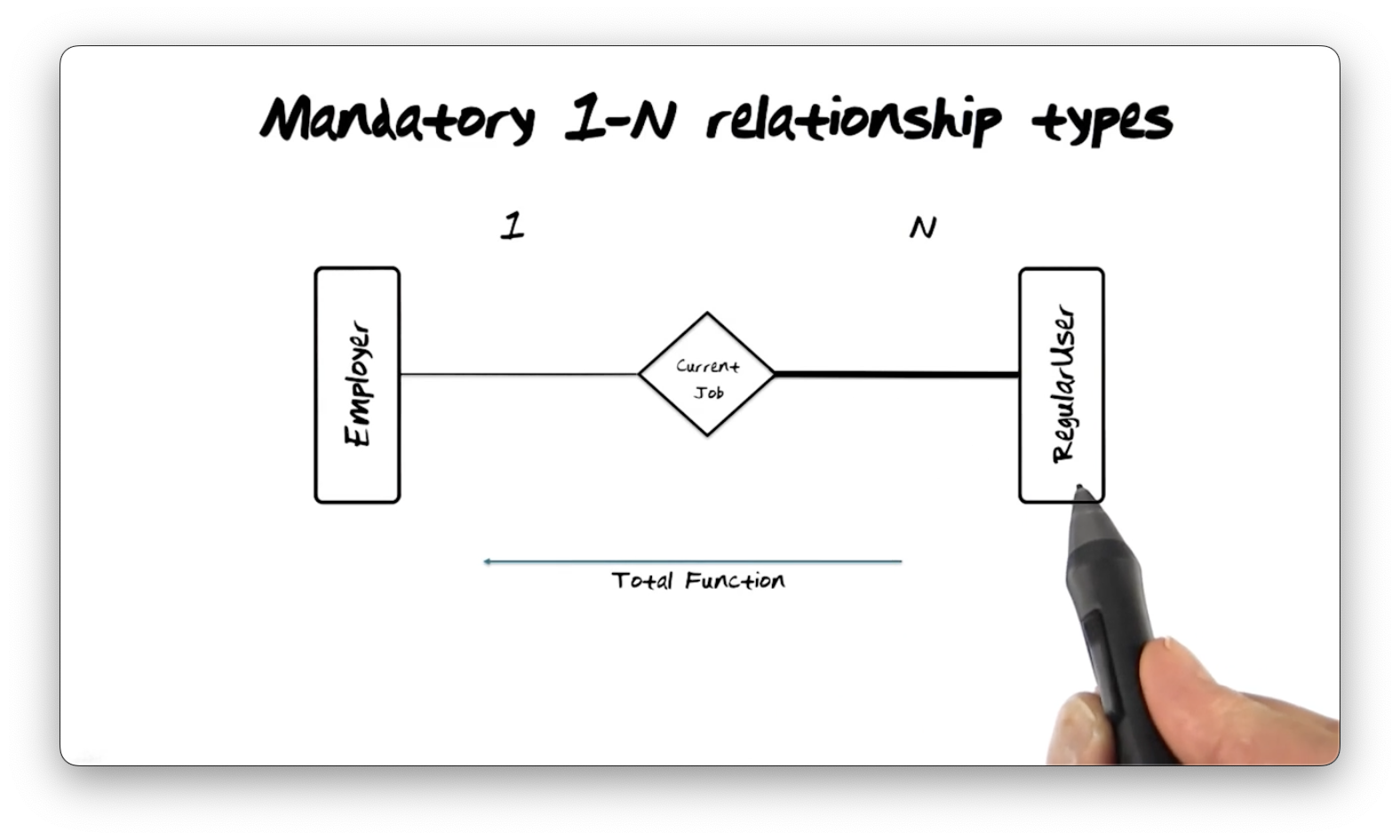
Mandatory 1-N Relationship Types

A variation of a 1-many relationship type is the mandatory 1-many relationship type, which we represent with a bold solid line.

In the diagram below, each instance of RegularUser must participate in the Current Job relationship. Some employers may still not have employees, but unlike before, each user must have a single employer. Since no user does not map to an employer, the mandatory 1-many relationship type is a total function.

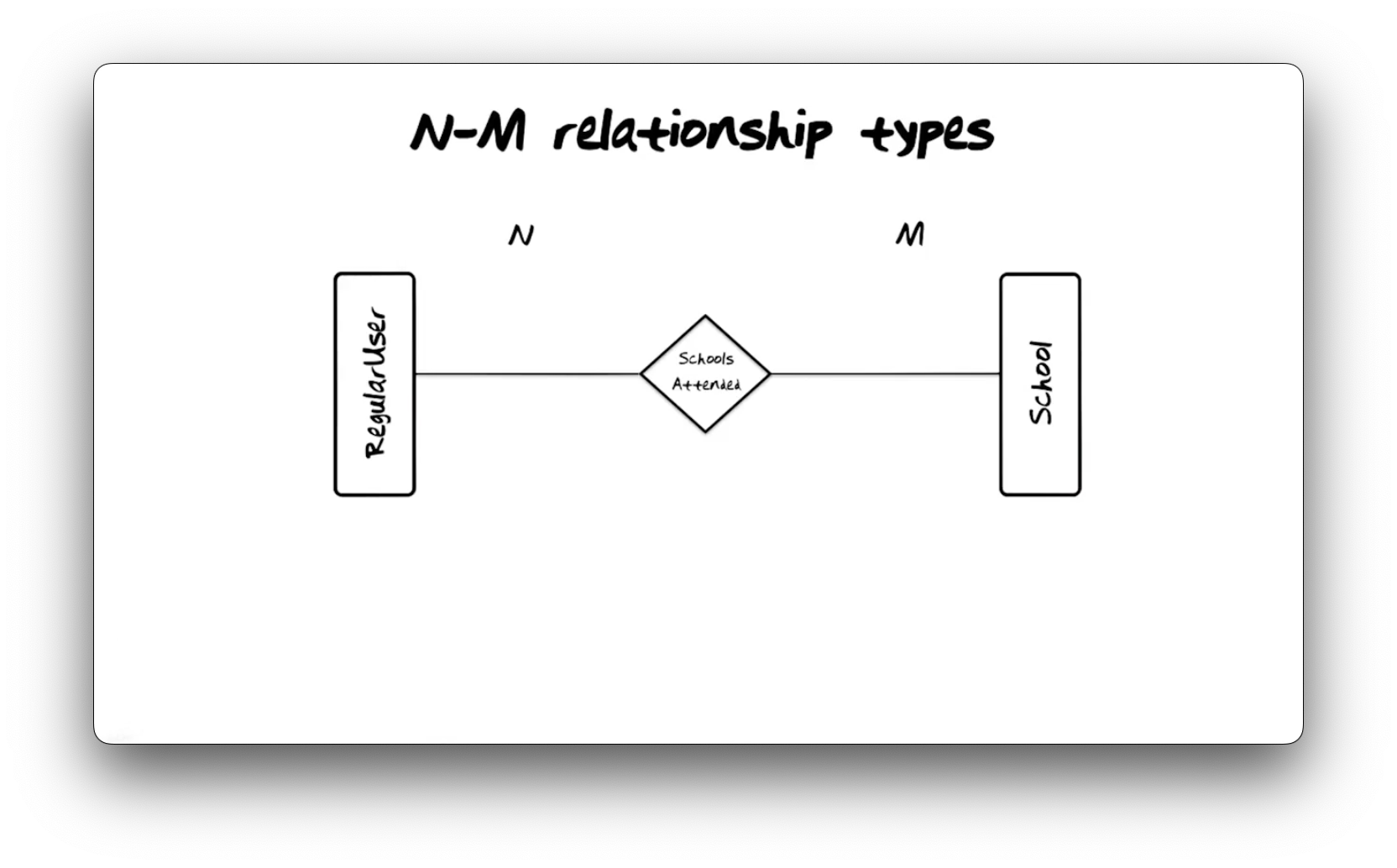
N-M Relationship Types

In a many-many relationship type or N-M relationship type, instances of entity types on either side of the relationship may associate with zero, one, or many instances of each other. As a result, we no longer have a function but rather a mathematical relation between the two entity types. Pictured below is the SchoolsAttended N-M relationship type connecting the RegularUser and School entity types.

N-ary Relationship Types

We have only examined binary relationship types - those that exist between two entity types - thus far. We now turn our attention to N-ary relationship types where N > 2.

Consider the following Event Team Member relationship type, a ternary (N = 3) relationship type, which relates the Event, Team, and RegularUser entity types.

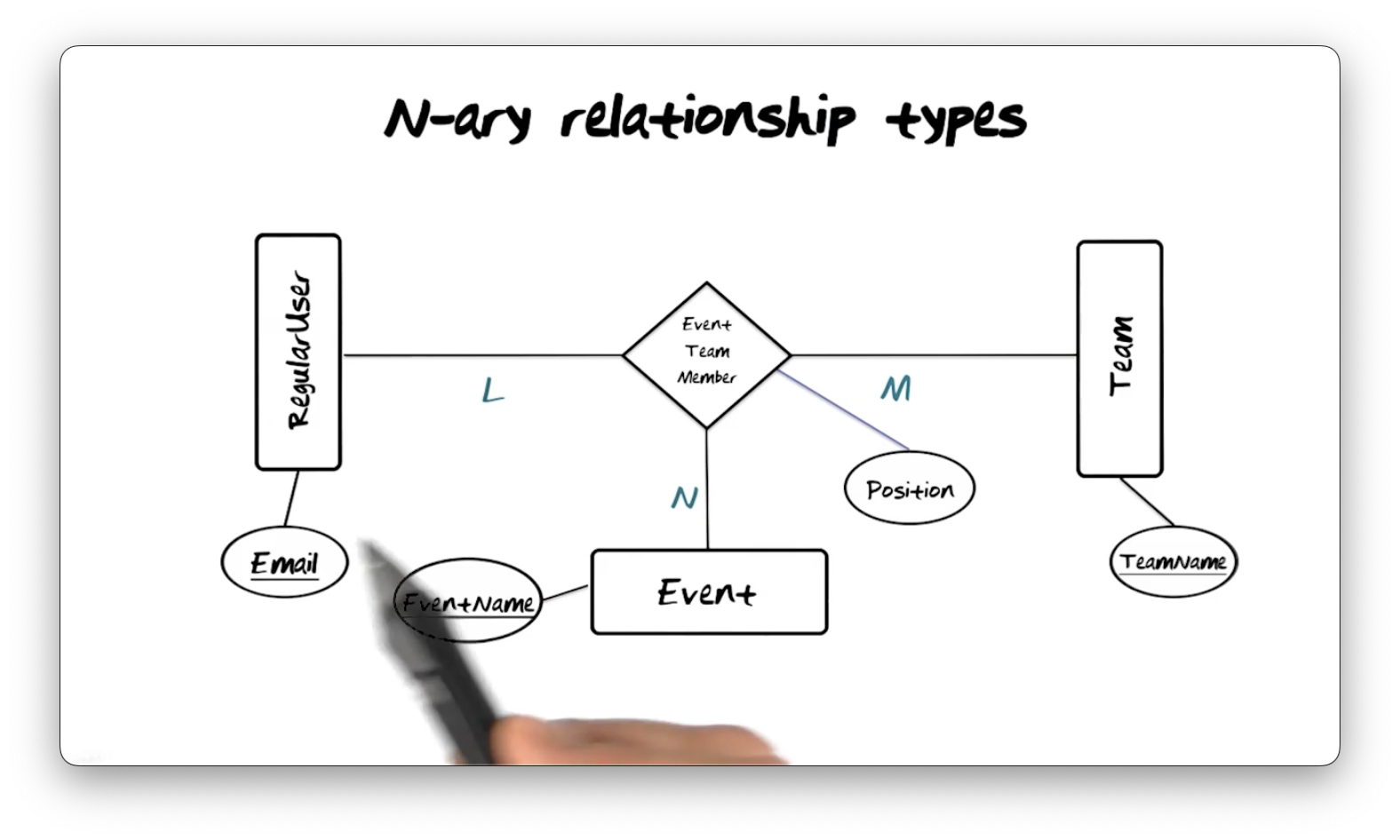
Assume we have just one instance of the RegularUser entity type and one instance of the Event entity type. We can associate M instances of the Team entity type for this instance pair; in other words, a given user in a given event can participate in M teams.

Assume we have just one instance of the RegularUser entity type and one instance of the Team entity type. We can associate N instances of the Event entity type for this instance pair; in other words, a given user on a given team can participate in N events.

Assume we have just one instance of the Team entity type and one instance of the Event entity type. We can associate L instances of the RegularUser entity type for this instance pair; in other words, a given team in a given event can have L users.

An instance of the Event Team Member relationship type describes an association among a RegularUser, Team, and Event instance. We need a tuple of Email, EventName, and TeamName property type values to precisely identify a single instance of this relationship type.

N-ary relationship types, N > 2, are rare in the real world because they are difficult to understand and explain. Unfortunately, it's not always possible to take an N-ary relationship type and decompose it into a set of binary relationships.

Many Relationship Types

Let's revise the Event Team Member relationship type above into a collection of three binary relationship types: User Team, which relates instances of User and Team; User Event, which relates instances of User and Event, and; Team Event which relates instances of Team and Event.

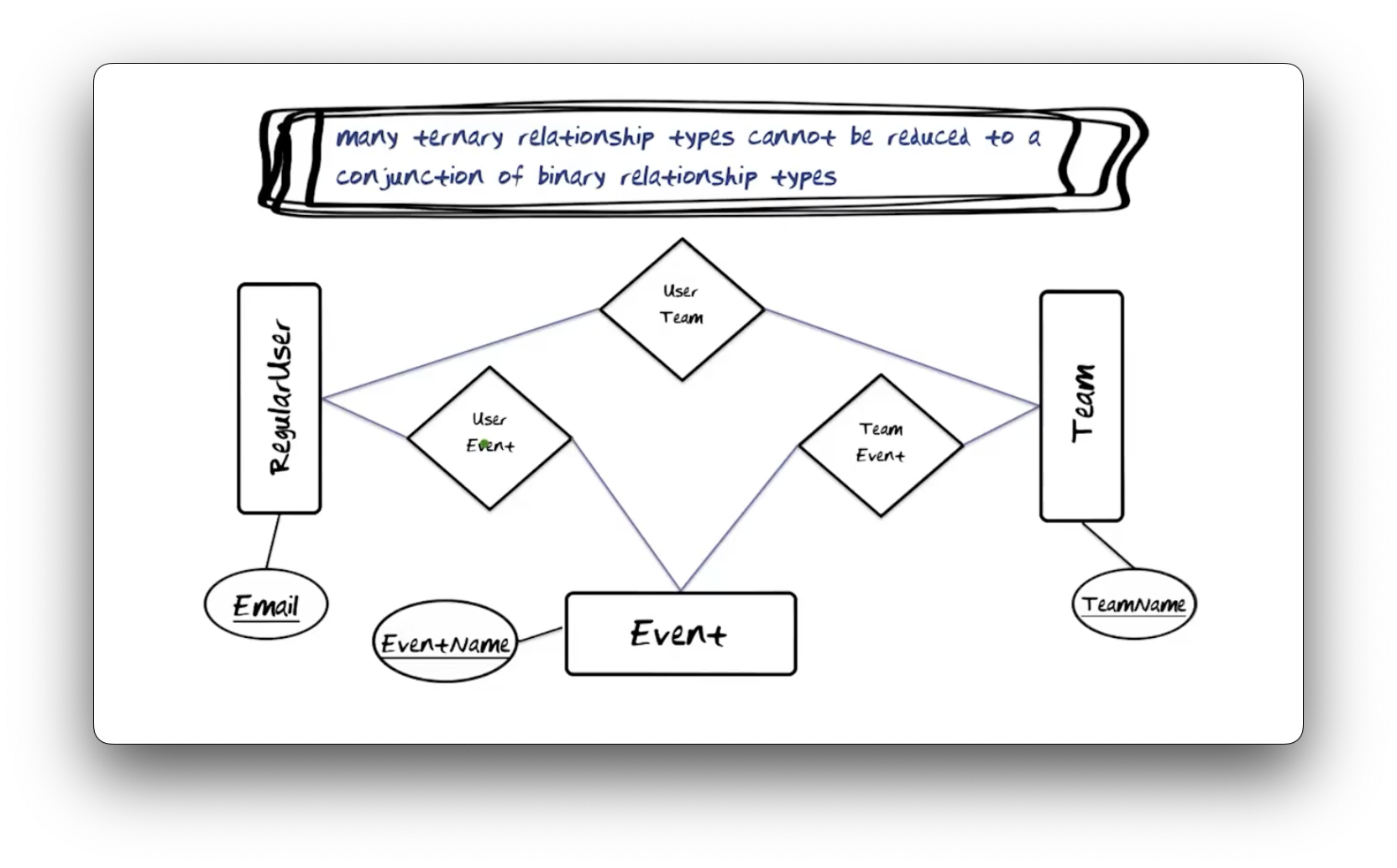
Assume we have one instance each of RegularUser, Team, and Event. We can associate a user with a team, a team with an event, and a user with an event, but we've lost the ability to model one user on one team participating in one event.

For example, we can say that John plays for the Yankees, John plays in the World Series, and the Yankees play in the World Series, but we cannot express explicitly that John plays for the Yankees in the World Series.

Identifying Relationships

We want to model a Twitter-like system where users can post multiple daily status updates. Consider the Posted relationship type below, which relates the RegularUser and StatusUpdate entity types. RegularUser has an identifying property type Email, and StatusUpdate has a property type DateAndTime.

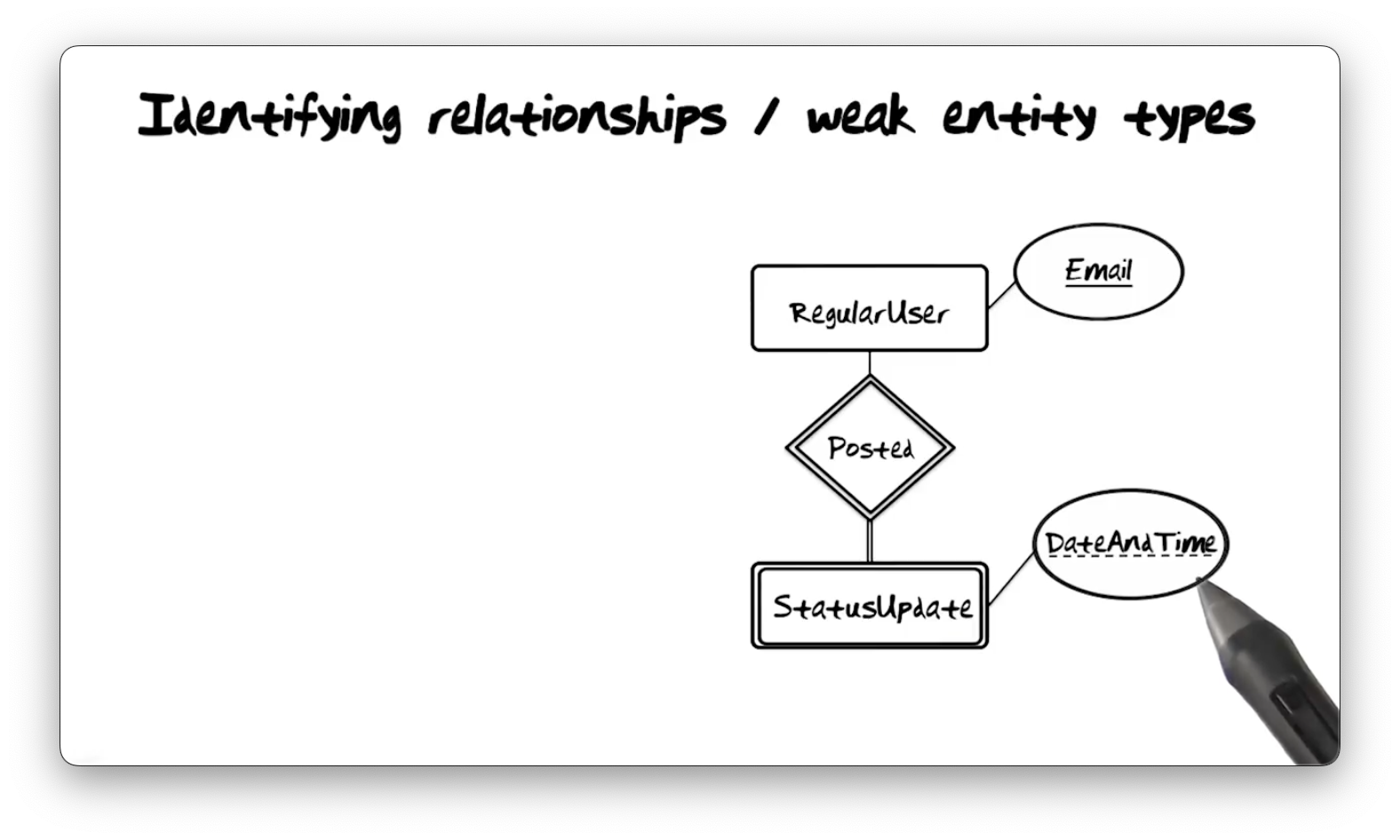
Since multiple users can create status updates simultaneously, DateAndTime is insufficient to identify StatusUpdate. We call DateAndTime a partial identifier. To completely identify a StatusUpdate, we need both the DateAndTime value and the Email property type value of the associated RegularUser instance.

We are assuming that DateAndTime has fine enough granularity such that a single user cannot create two status updates simultaneously.

A StatusUpdate cannot exist without the associated RegularUser; therefore, we refer to StatusUpdate as a weak entity type. The Posted relationship type is an identifying relationship type because, to identify StatusUpdate, we must use information about the related User - specifically, their email address.

We represent partially identifying property types with dotted underlines, weak entity types with double rectangles, and identifying relationship types with double diamonds.

Recursive Relationship Types

A recursive relationship type relates an entity type to itself. Here we have an AdminUser entity type that participates in a Manages relationship type with another AdminUser in either the Supervisor or Supervisee role.

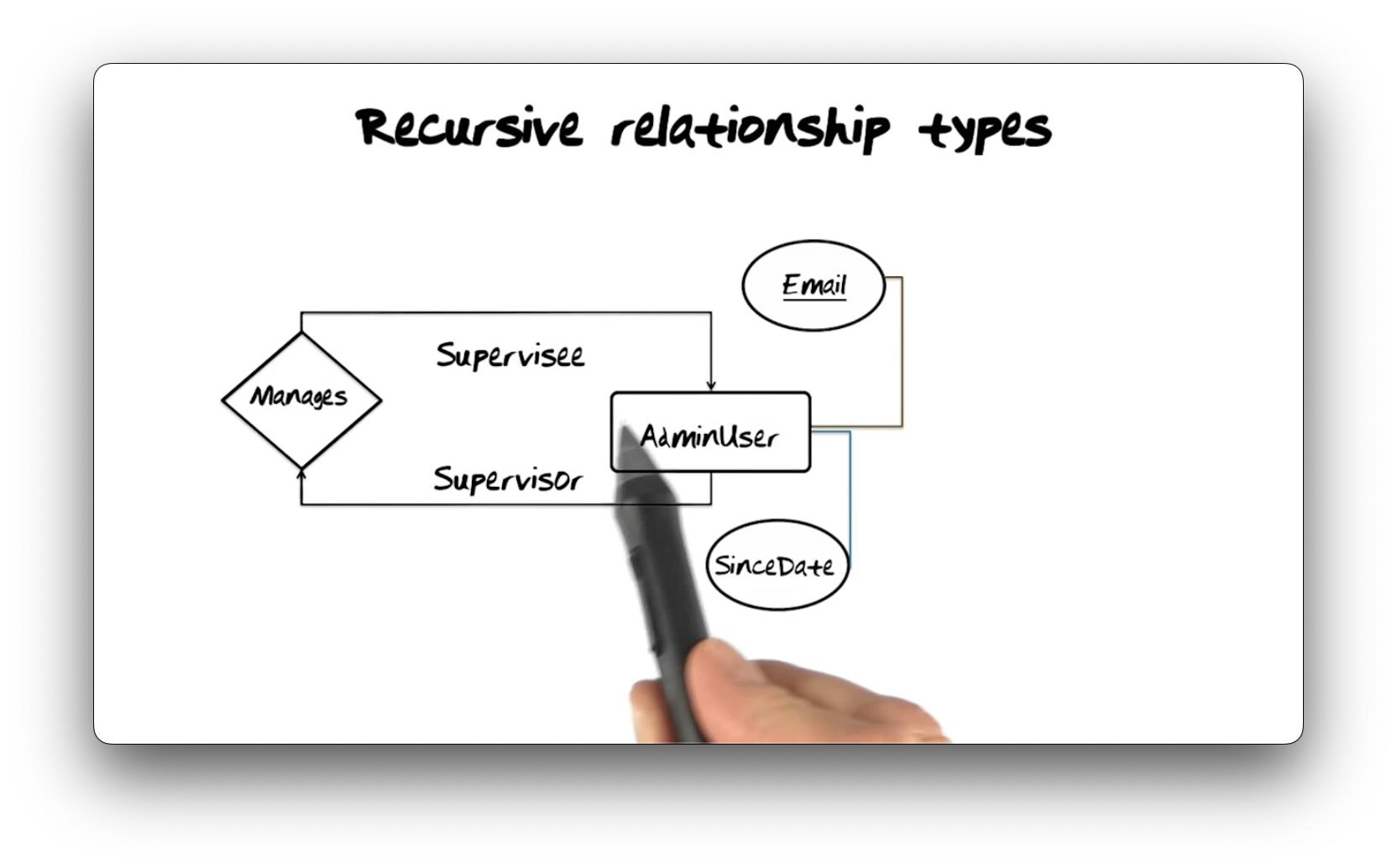
We represent recursive relationship types with arrowheads and roles, which add a logical direction to the relationship; in this example, a supervisor manages a supervisee, and both are admin users. Note that an admin user may be in multiple relationships with other admin users, fulfilling the supervisor role in some and the supervisee role in others.

Supertypes and Subtypes

In this diagram, we have a User entity type that has four subtypes: RegularUser, AdminUser, Male, and Female. Any instance of these four subtypes is also an instance of User; in other words, User is the supertype of the subtypes.

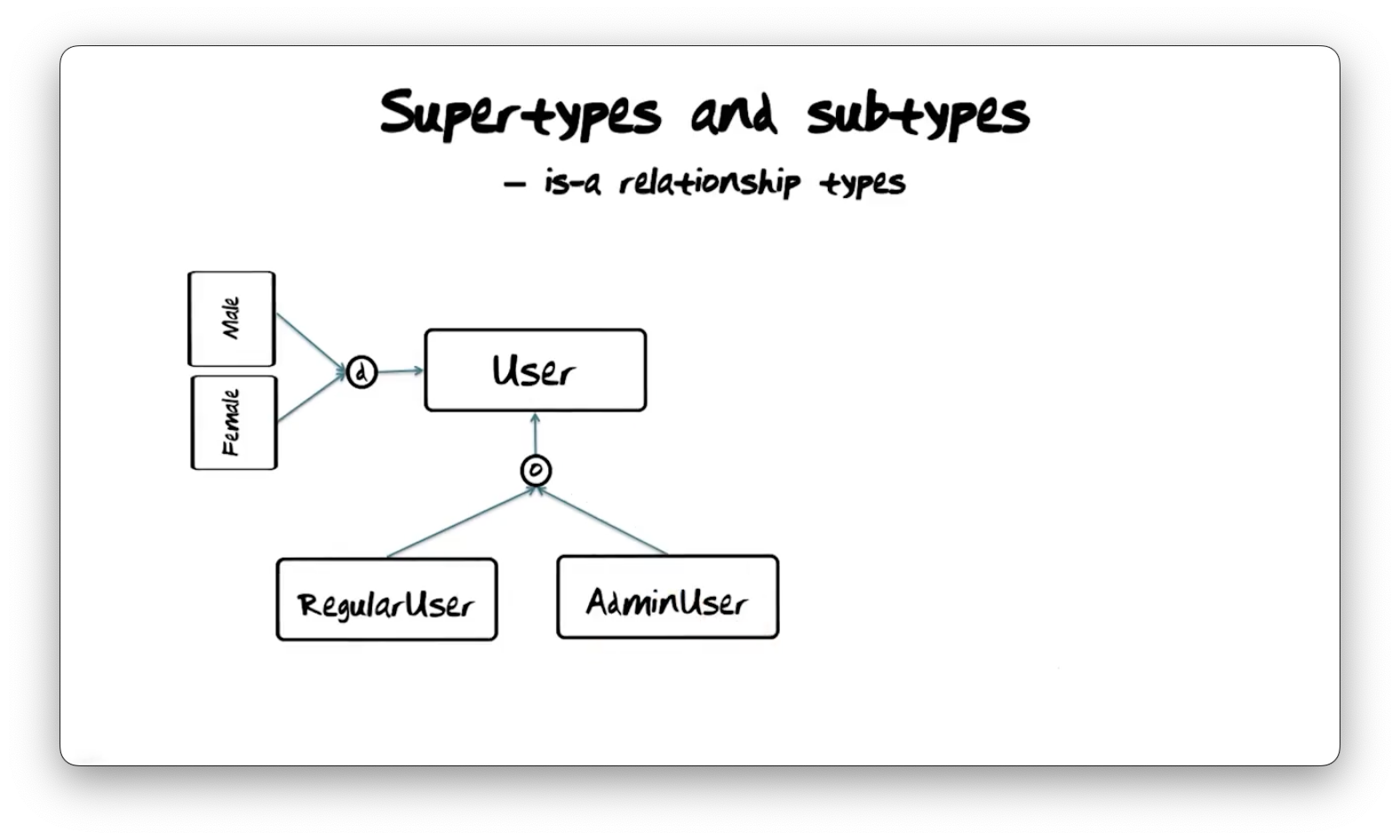
The sets of Female and Male instances are disjoint; in other words, there are no instances of User that are both Female and Male. We represent this disjoint requirement using a "d" in the diagram above. On the other hand, we allow instances of AdminUser to also be instances of RegularUser, and we represent this overlap using an "o".

Supertypes and Subtypes: Inheritance

Those familiar with object-oriented programming may see similarities between subtypes/supertypes and inheritance. Consider the User hierarchy again. The User supertype has an Email identifying property type and a Password property type. The four subtypes of User inherit these two property types from User.

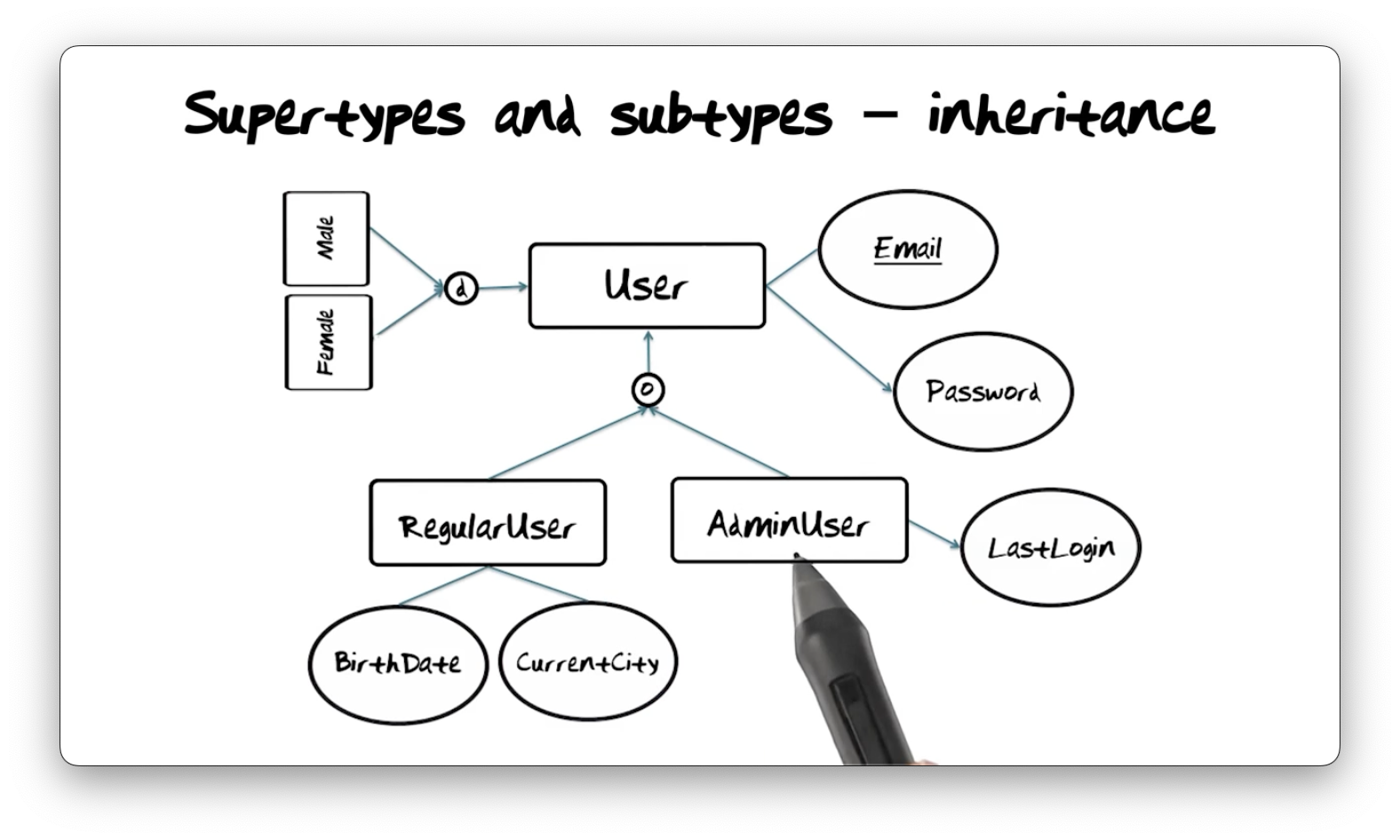
Subtypes can have local property types as well as inherited ones. For example, RegularUser has BirthDate and CurrentCity property types, and AdminUser has a LastLogin property type. Subtypes do not share their local property types with other subtypes or their supertype. In other words, RegularUser and AdminUser have Email and Password property types, but neither User nor AdminUser has the BirthDate property type.

Union Entity Types

Consider the following diagram, representing the Company, GovtAgency, and Employer entity types. Here, the Employer must be either a Company or GovtAgency. If the employer is a Company, it has the EIN property type (an EIN is an identifier for tax purposes). If the employer is a GovtAgency, it has an AgencyID property type, which composes the Municipality and AgencyName property types.

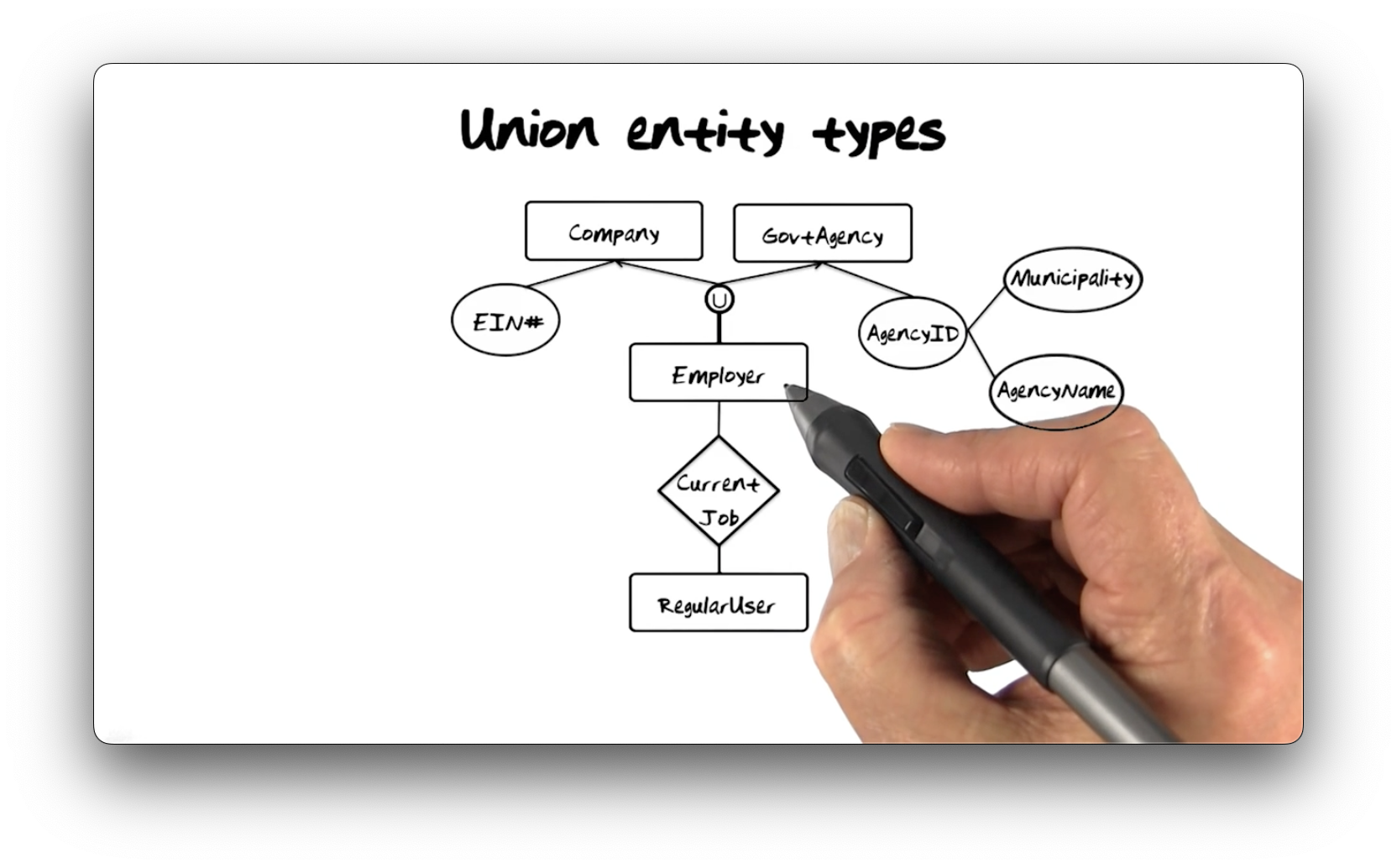
In this example, Employer is a union entity type. Union entity types have two rules. First, they must be a subset of the mathematical union of the comprising types. In other words, there will be no instances of Employer that are neither a Company nor a GovtAgency. Second, the intersection between the comprising types must be empty, i.e., an Employer can only be a Company or a GovtAgency, not both.

Thing, Relationship, Property

We have now seen notation to represent entities, properties, relationships, and constraints. But how do we really know if something is an entity, a property, or a relationship? How much does the definition of something depend on the context in which we perceive it? Furthermore, does the extended-entity relationship model support the fundamental types of abstraction we expect, including classification, aggregation, and generalization? Finally, why haven't we seen any queries? Where is the query type in the extended-entity relationship model?

Are Relationships Entities?

Are relationships entities, or are they just the "glue" that connects entities? Below we see an Employer entity type connected to a RegularUser entity type via a Current Job relationship type, which has a StartDate property type. If a relationship type has a property type, is it an entity type?

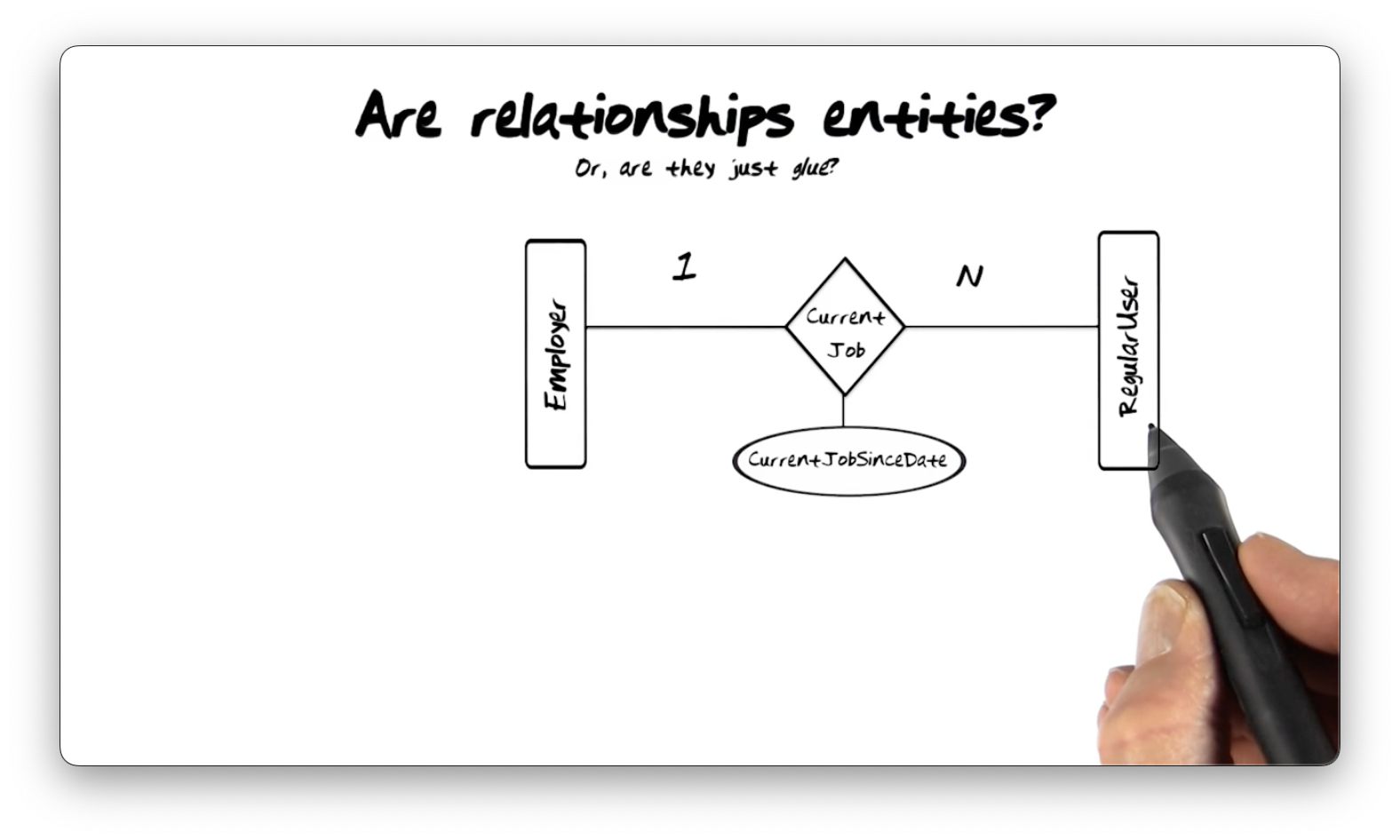
If we can't accept that relationship types have property types, we must move StartDate to either Employer or RegularUser. RegularUser is the more sensible candidate here: each user likely started work on a different date. Instead, if we moved StartDate to Employer, we would be saying that every employee under a particular employer has the same start date, which doesn't make sense.

Generally, in 1-1 or 1-many relationships, we can move property types from the relationship type to the connected entity types.

Another Example

Sometimes we need to convert a relationship type into an entity type, known as an objectified relationship type. In the following diagram, we objectify the Schools Attended relationship type and add a GPA property type. We model two new relationship types to achieve the same cardinality between School and RegularUser as the original N-M mapping: a 1-N relationship type between Schools Attended and RegularUser, and a 1-M relationship type between School and Schools Attended.

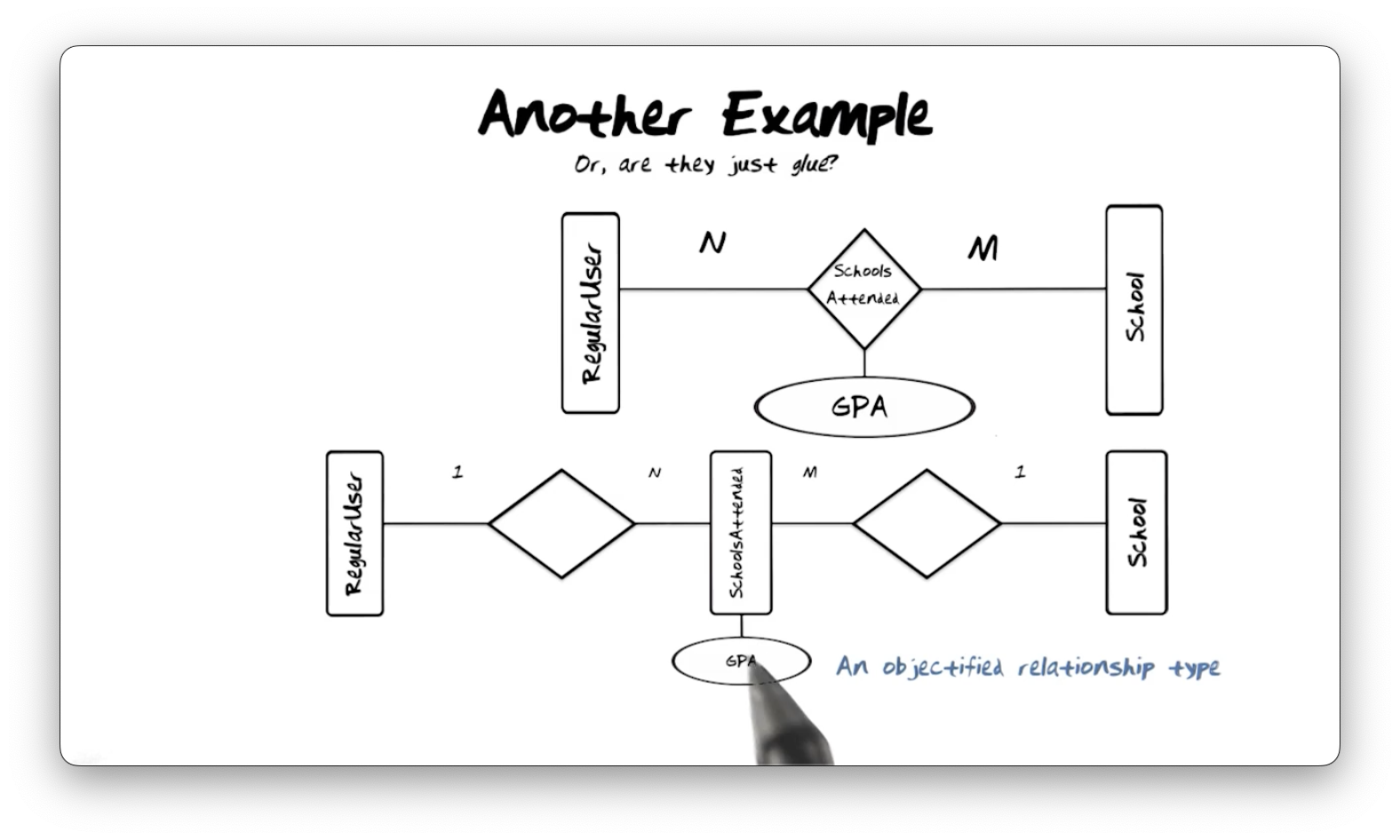
Messing with your Brain

Suppose we model a system containing information about users and their last names. At first glance, we might model a User entity type and a LastName property type. Is this correct?

What's in a name? Names can convey geographical information: for example, "Andersen" is Danish, while "Anderson" is Swedish. Names can convey genealogy - the Icelandic names Haraldsdottir and Helguson mean son of Harald and daughter of Helga, respectively. Names like Carpenter, Baker, and Smith may convey occupation, while names like Ifran, Sabir, Peter, and Paul may convey religion.

The point here is whether LastName is an entity type or a property type depends on the system we want to model. In many applications, last name may be a property type, but an entity type is more appropriate in others, such as those concerned with genealogy.

Relationship Type or Entity Type

Suppose we model a system containing information about users and weddings. At first glance, it might seem obvious that we have a User entity type and a Wedding relationship type.

From a wedding planner's perspective, the following might be important:

• wedding dress
• honeymoon location
• florist
• caterer
• wedding singer
• limo provider

From the wedding planner's perspective, the most important thing is the wedding, and thus that ought to be the entity type. Context is crucial when we attempt to fix and represent a perception of reality. We cannot assume that an object of one type - entity, property, relationship - in one system must be the same type of object in another.

What can the EER Do?

Three types of abstraction are generally agreed upon as important to fix perceptions of reality: classification, aggregation, and generalization. The extended entity-relationship data model supports classification by allowing us to define entity types and supports generalization through supertypes and subtypes. Does it support aggregation?

Car Graphic

Aggregation refers to the ability to compose multiple substructures into a cohesive whole. For example, the drivetrain pictured below is composed of an engine transmission, and driveshaft, among other components. Unfortunately, The extended entity-relationship model does not support aggregation.

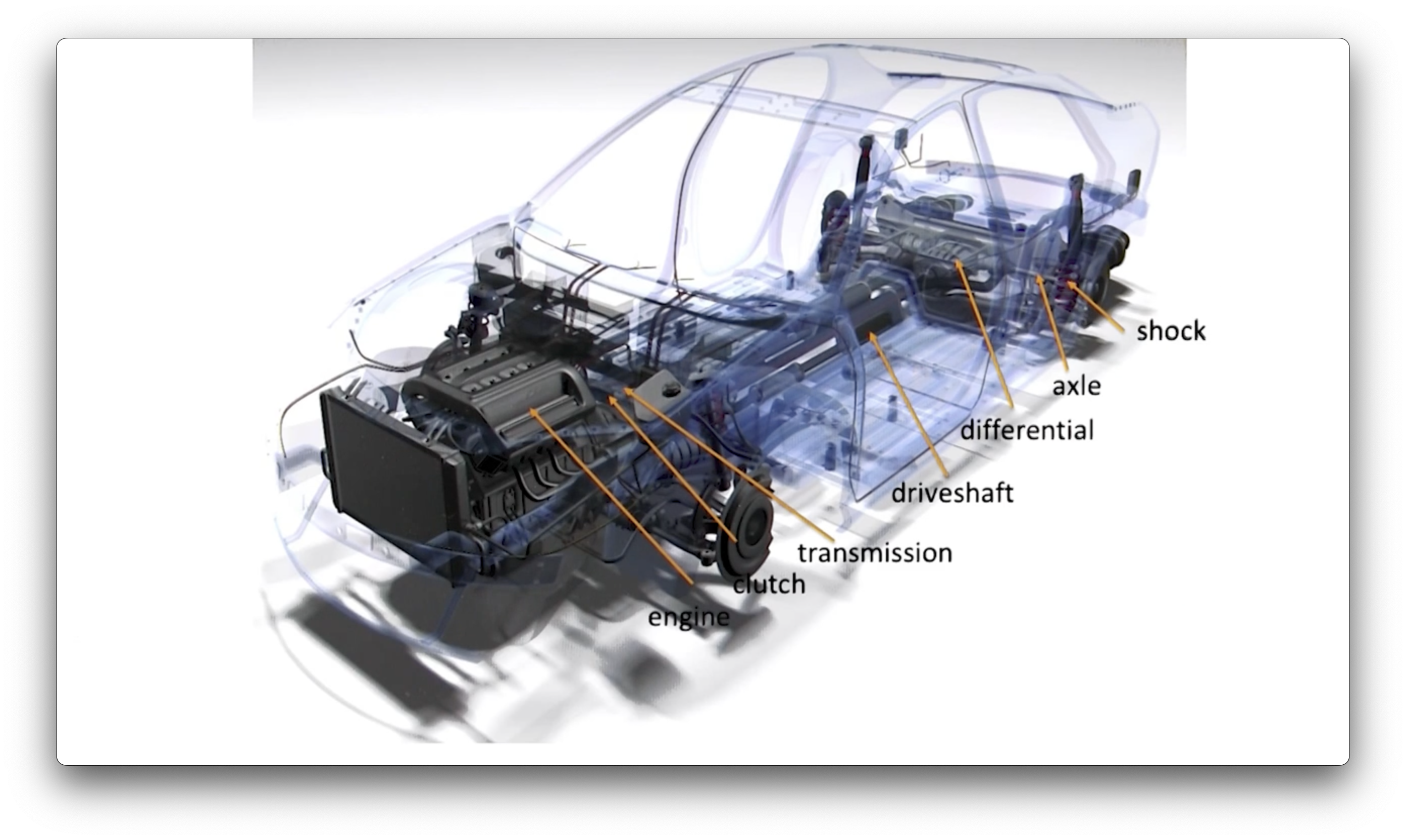
What's the Result Type of a Query

As we said, data models such as the extended entity-relationship model consist of formalisms to express data structures, constraints, and operations. Does the extended-entity relationship model have a type for the result of a query?

EER Diagram

Consider the extended entity-relationship diagram below. Suppose we want to print a list that includes each regular user's email, first name, last name, and the name of each school they attended.

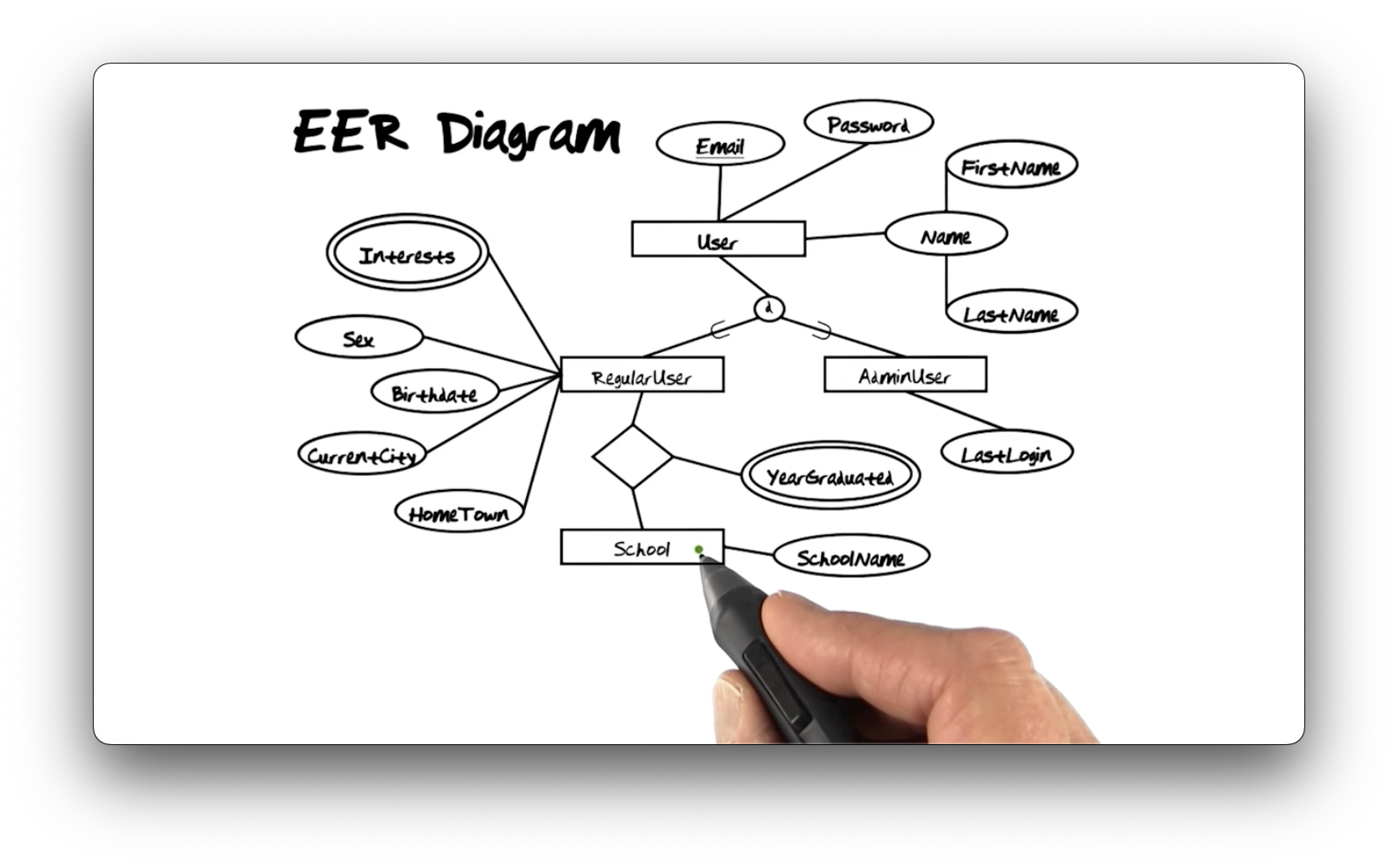
What is the return type of this query? It's a list of properties, but that list doesn't have a type that we can operate on - it's not an entity type, property type, or relationship type. The essential observation here is that since the result doesn't have a type, there is no way we can continue to operate on it.

Query languages must be closed; in other words, operations performed against objects of a particular type must produce objects of the same type. In the extended entity-relationship model, we query entity types, property types, and relationship types and, in this case, receive a list of values. In the relational model, which we will see shortly, we query relations and those queries produce relations that we can further query. The lack of a closed query language for the extended entity-relationship model explains why no database management systems implement it.

Relational Model Theoretical Foundation

The extended entity-relationship model is great for fixing and representing perceptions of reality, yet no commercial database systems implement this model. Instead, they implement the relational data model, so we must first define a relation and then map extended entity-relationship components onto relations.

Relational Model

Whenever we learn a new data model, we need to focus on three different pieces: data structures, constraints, and operations.

We can express operations in relational databases using two different notations: relational algebra and relational calculus. Relational calculus itself contains two notations: tuple calculus, which operates on tuples of relations, and domain calculus, which operates on cells of domains. SQL is a tuple calculus language.

Data Structures

Unlike the extended-entity relationship model, the relational model only has one data structure, the relation. We use relations to represent entities, properties, and relationships.

A domain is a set of atomic values we use to model data. From the perspective of the database management system, an atomic value is indivisible. We can think of the set of atomic values as a type. For example, all character strings from length zero to length fifty comprise the varchar(50) domain.

A relation, $R$, is a subset of the set of ordered $n$-tuples, such that each element, $d_i$, in the tuple is an element of the corresponding domain, $D_i$. It is absolutely essential to understand that a relation is a set. Formally,

$$ R \subseteq {<d_i, d_2, ... ,d_n> \mid d_i \in D_i, i=1, ..., n} $$

An attribute, A, is a unique name given to a domain to explain or interpret its role in a specific relation. With attributes, we can refer to columns in a relational database by name instead of solely by position.

Big Deal

We illustrate relations using tables. Consider the following table. The relation name is RegularUser, which has five attribute names: Email, BirthDate, CurrentCity, Hometown, and Salary. The domains they are defined over are varchar(50), datetime, and integer.

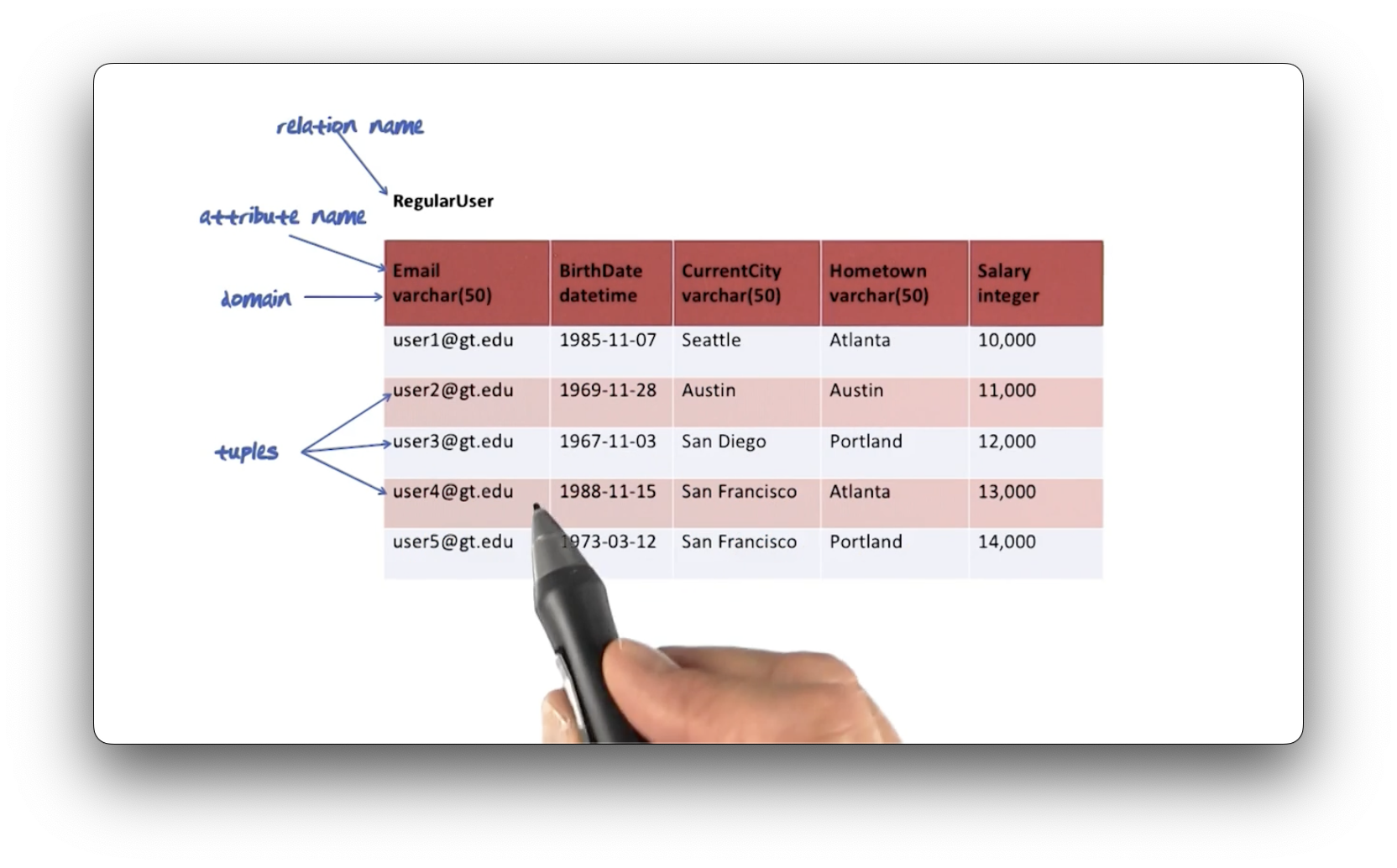
The number of attributes, or columns, is called the degree of the relation. The number of tuples in the relation is the cardinality. This table has a degree of five and a cardinality of five.

The value of the relation is independent of attribute order and tuple order, and we will see why this is such a big deal soon.

Constraints

Consider the tables below. We have a general User table with Email and Password columns, which represents the list of users in reality about whom we are capturing information in this database. We also have a RegularUser table with Email, Birth Year, Sex, Current City, and Hometown columns.

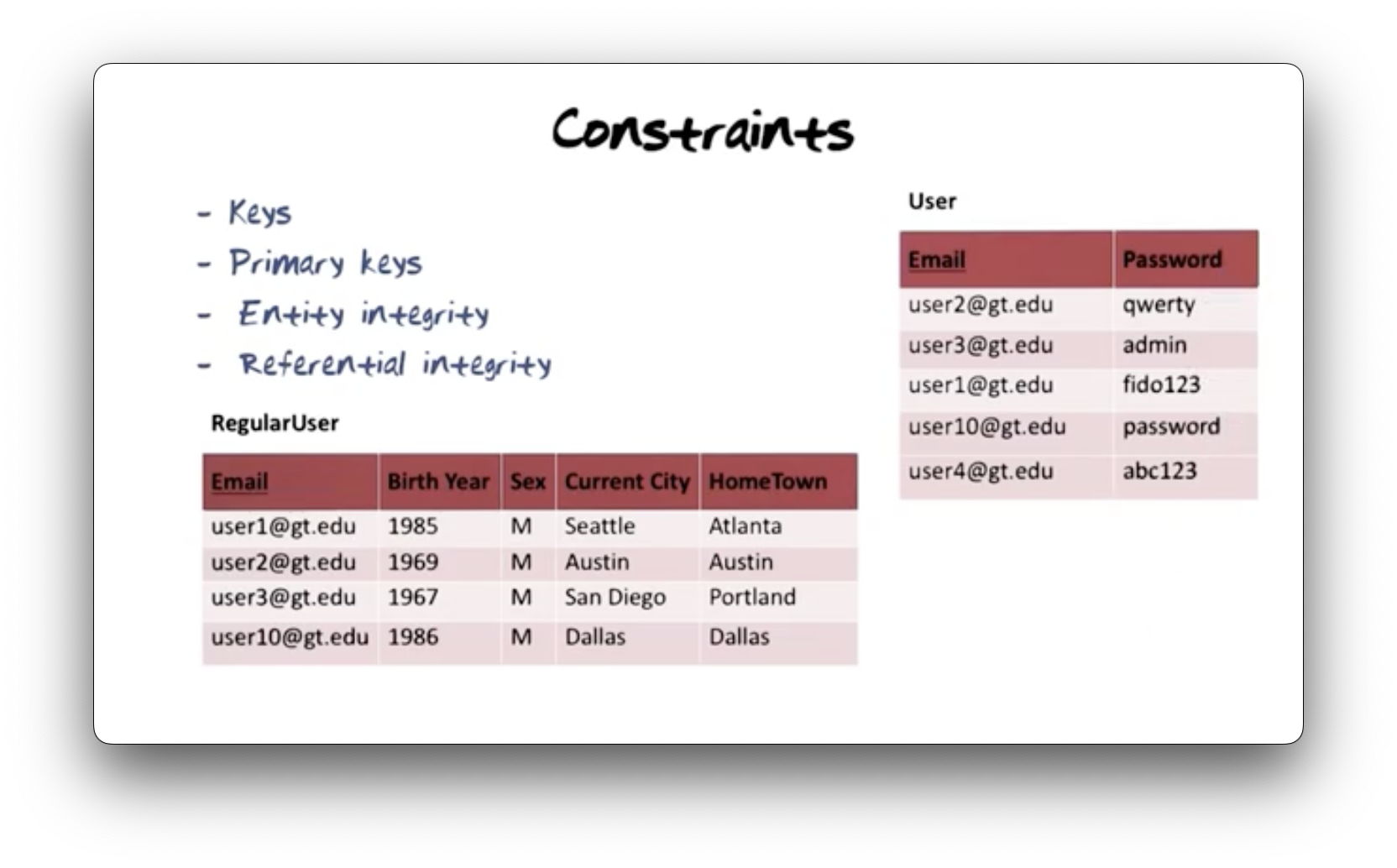
We have chosen emails as the unique identifier, or primary key, for rows in the User table (as opposed to relying on system-generated surrogates). Entity integrity requires that primary keys cannot be null: every user must have an email address.

The Email column in the RegularUser table is also a key, in that it uniquely references users in the User table. Referential integrity requires that the set of emails in the RegularUser table must be a subset of the emails in the User table. We cannot reference a user that does not exist in our primary table.