EER Relational Mapping

Entity Types

Let's now explore mapping the entities, properties, and relationships from the extended entity-relationship model to relations. Suppose we have an entity type named ET. We can create a corresponding relation named ET. If the entity type has an identifying property type A, then the relation will have a primary key A. If the entity type has a property type B, then the relation will have an attribute B.

Suppose the entity type has a composite property type C, composed of D and E. In the relation, we add attributes D and E, but what happened to property type C? In the translation, we lose this property type and, therefore, the context it provides. For example, if C is Name, D is FirstName, and E is LastName, we lose the notion of Name composing FirstName and LastName when building the relation.

Ideally, we want C to survive the transformation. However, we defined relations as a subset of tuples constructed from domains with atomic values, not composite values. The relational model is inherently flat, and the languages we will look at - relational algebra, relational calculus, and SQL - only work when this constraint holds.

Multi-Valued Property Types

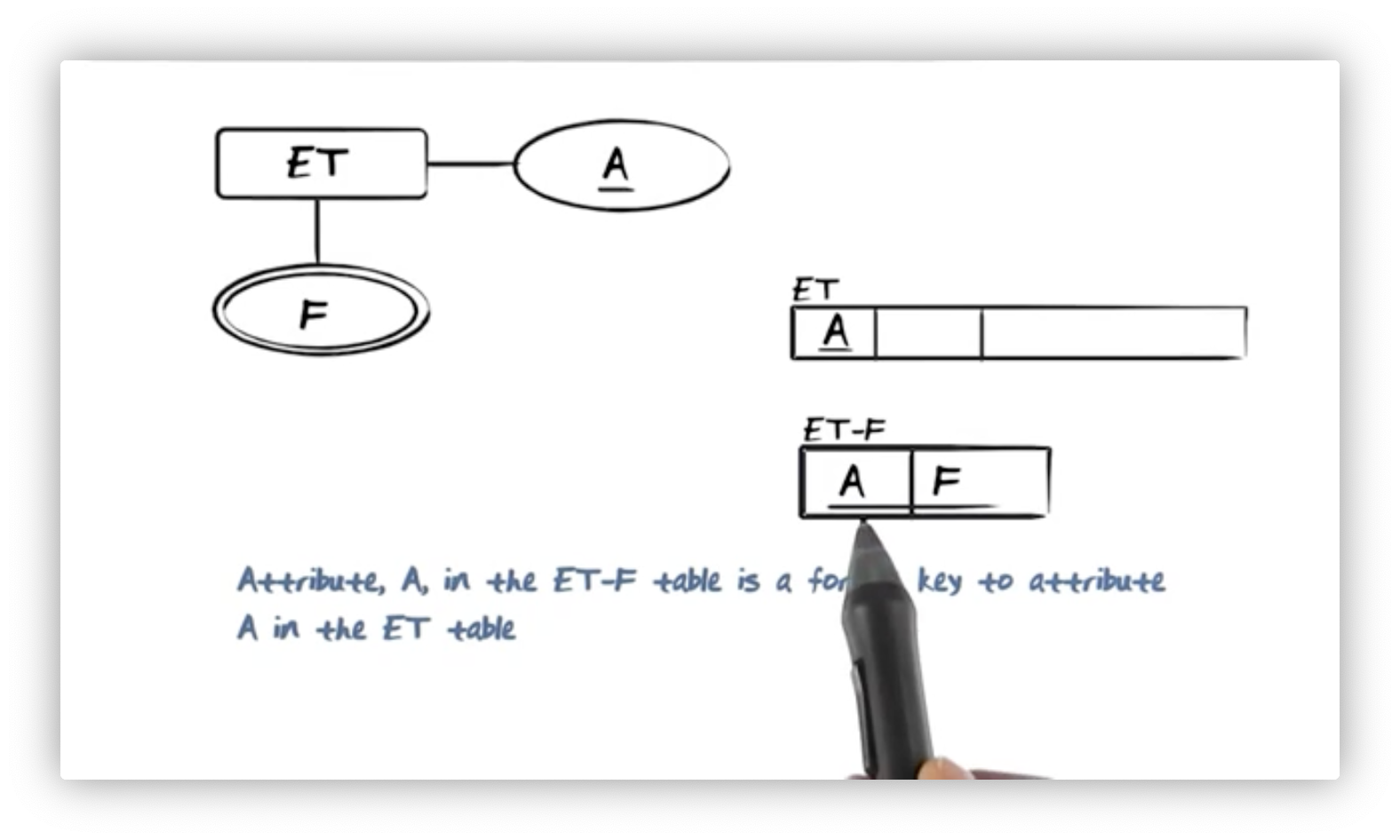
Consider the entity type ET with identifying property type A. From a previous example, we saw that we could create a corresponding relation named ET with primary key A. Now let's suppose ET has a multi-valued property type F.

The relational model doesn't support multi-valued attributes, so we cannot directly add F as an attribute on ET. Instead, we create a new relation, ET-F. ET-F contains attributes A, which is a foreign key on A in ET, and F, which holds a single value of F for the ET identified by A.

The combination of A and F in ET-F forms a composite key for ET-F. Remember, a given instance of ET will have a unique value for A, and we can associate that value with multiple different values of F so long as the combination is unique. Of course, the values of A in ET-F must be a subset of those that exist in ET.

The point to remember here is that in the relational model, instead of creating an attribute that takes multiple values, we create multiple tuples in a new relation that all reference the original relation.

1-1 Relationships

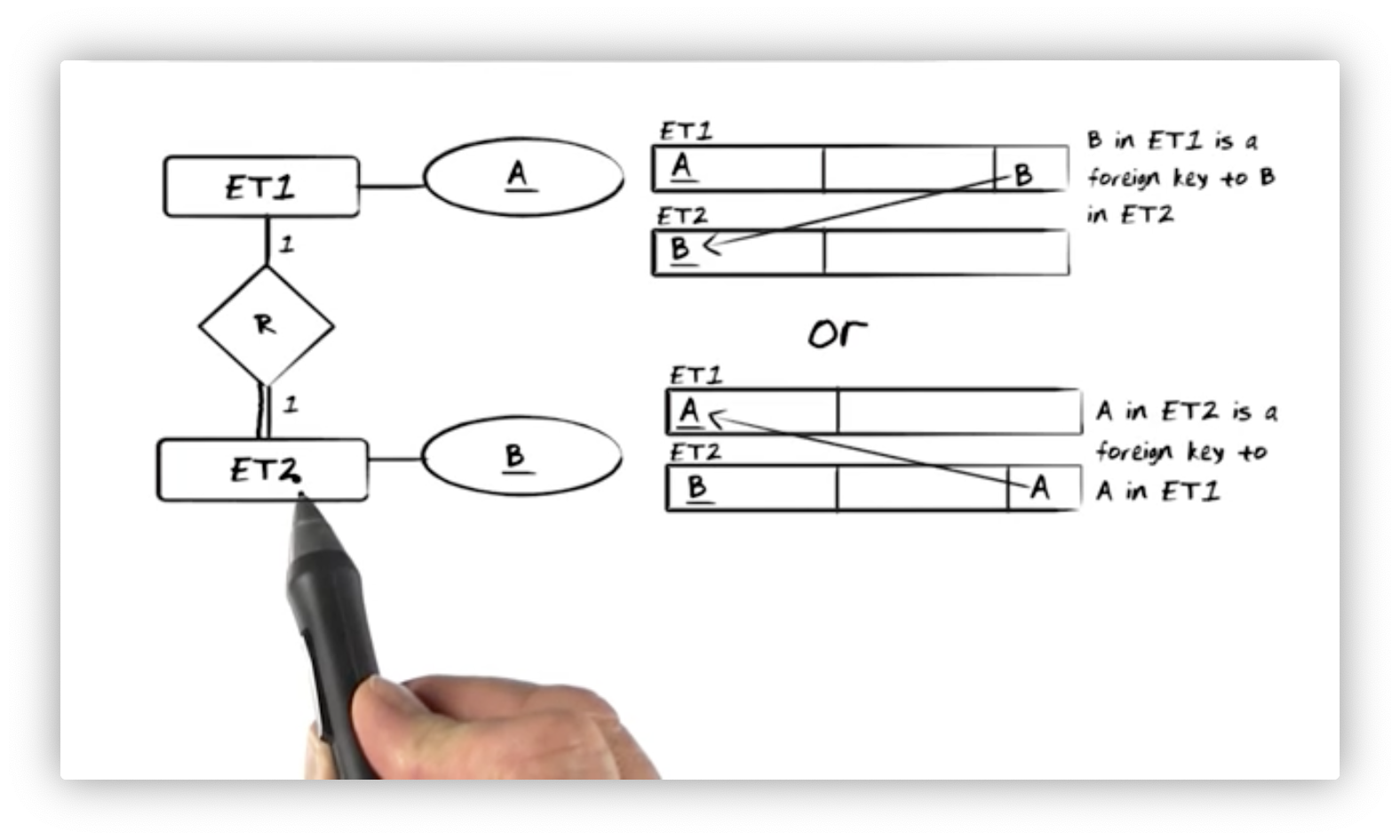
Suppose we have entity type ET1 with identifying property type A, entity type ET2 with identifying property type B, and a 1:1 relationship type R that connects them.

We start by creating a relation ET1 with primary key A and relation ET2 with primary key B. We need some mechanism to associate these relations, and there are two approaches we can take. In ET1, we can insert the primary key of ET2, B, as a foreign key in ET1 to connect the two relations. Alternatively, we can insert the primary key of ET1, A as a foreign key in ET2 to form the connection.

Both solutions are acceptable in this most basic example, but we require one configuration over the other in many cases. For example, suppose that ET2 must mandatorily participate in R. Every instance of ET2 in the database must connect to ET1; put another way, we cannot have an instance of ET2 that doesn't reference ET1. In this case, ET2 must hold the reference. We cannot ensure that all instances of ET2 are referenced in ET1 otherwise. Of course, ET2 must additionally have a non-NULL constraint on the foreign key.

1-Many Relationships

Let's suppose now ET1 and ET2 are in a 1-N relationship, where one instance of ET1 relates to many instances of ET2. Consider the two representational options we saw above: should the ET1 relation reference ET2 or should ET2 reference ET1?

We have a unique value for A for each instance of ET1, and we must associate multiple instances of ET2 with that key. As we saw earlier, the relational model does not allow multi-valued attributes, so these references cannot live in ET1. We need the ET2 relation to hold the foreign key. Note that this solution only works because the ET2 instance can only associate with at most one ET1 instance.

Many-Many Relationships

If ET1 and ET2 are in an N-M relationship, R, we appear to have a problem. We already saw that we could not reference ET2 from ET1 since that would require a multi-valued attribute. But now we cannot reference ET1 from ET2 for the same reason. To solve this problem, we need to generate a particular relation for R, which stores references to the primary keys A of ET1 and B of ET2.

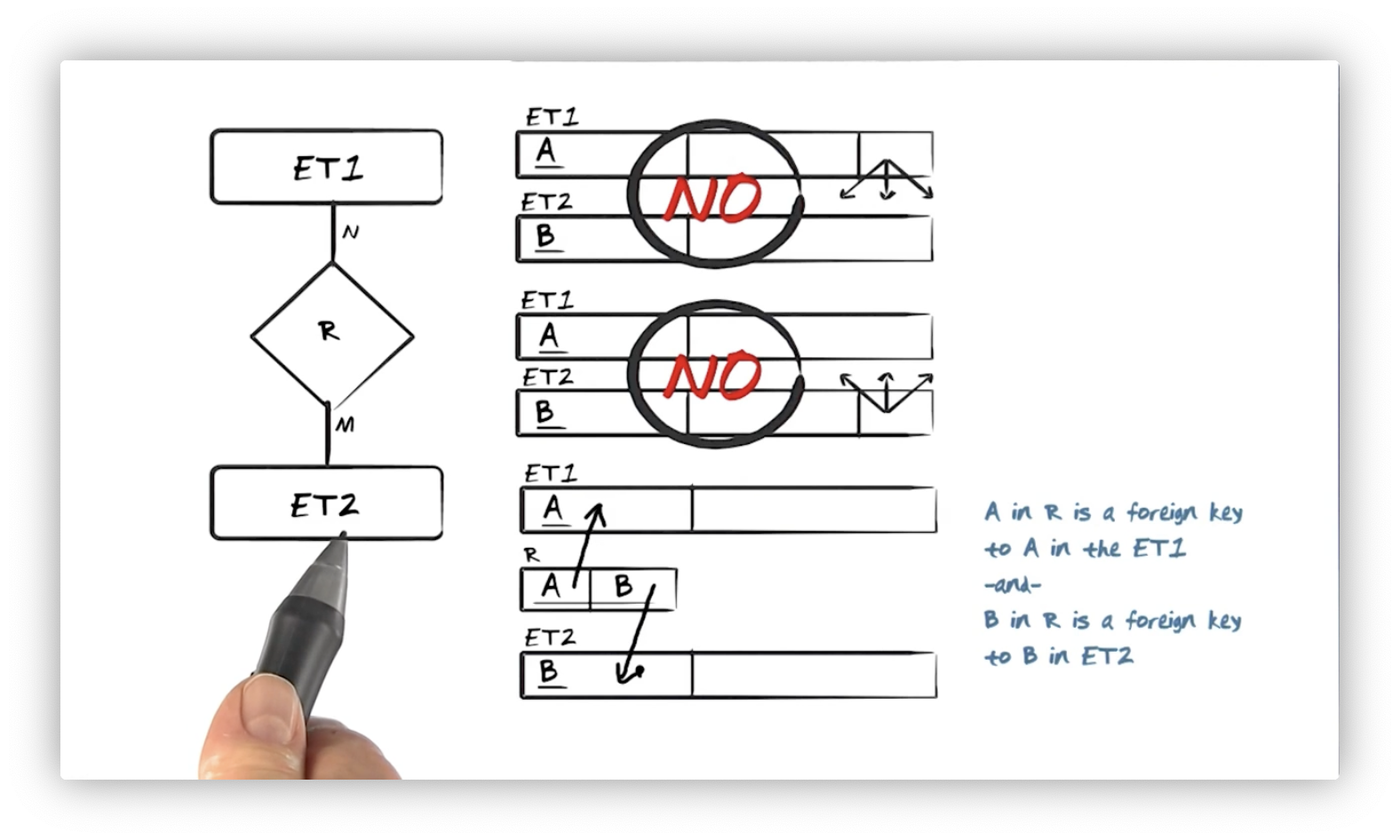
For a tuple in ET1, there may be multiple tuples in R referencing its key, A, each with a unique value of B identifying a tuple in ET2. Vice versa, for a tuple in ET2, there may be multiple tuples in R, referencing its key, B, each with a unique value of A identifying a tuple in ET1. The combination of A and B constitutes the key in R, representing the relationship between one ET1 and ET2 instance.

Weak Entity Types and Identifying Relationships

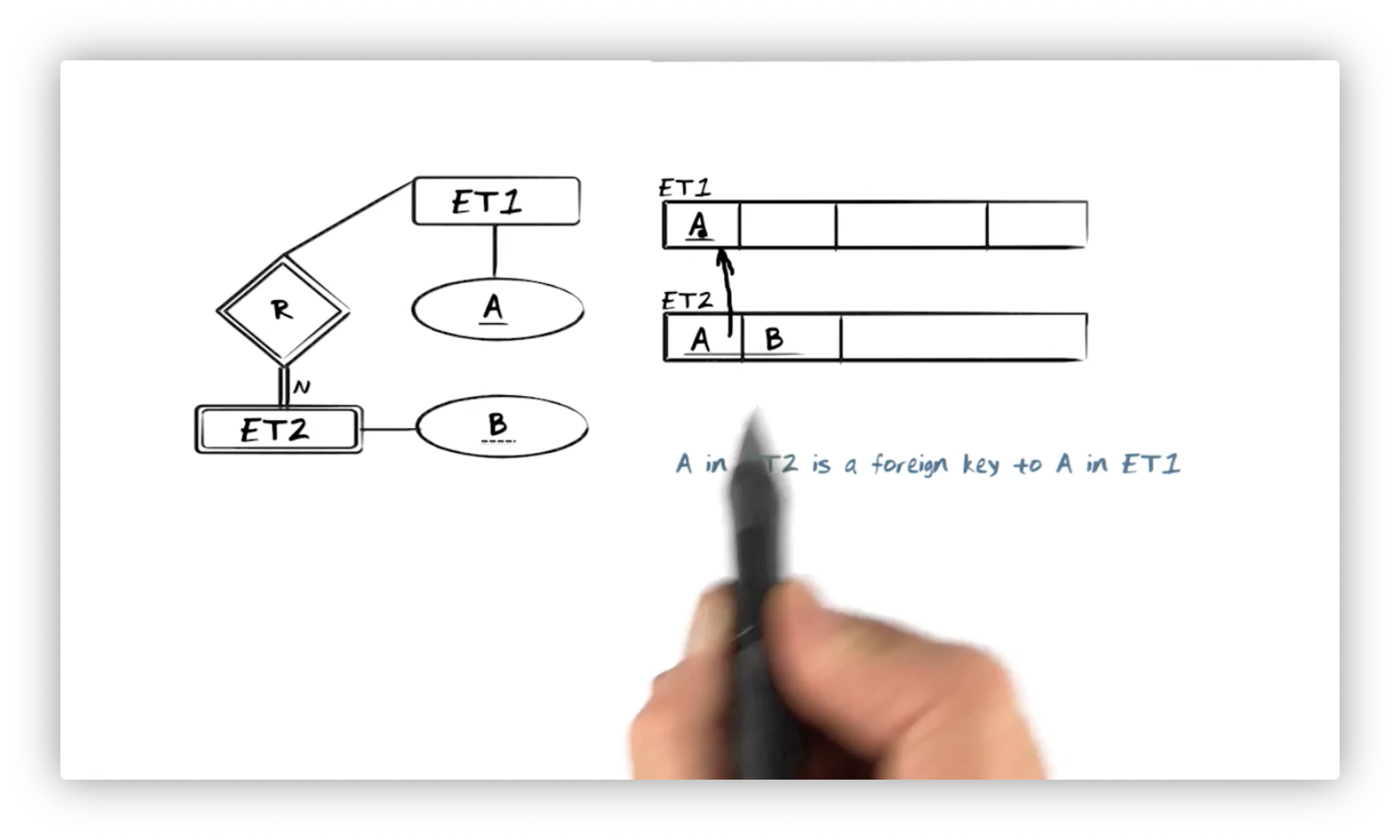
Let's look at an identifying relationship type, R, between a weak entity type, ET2, with weakly identifying property type B and an entity type, ET1, with identifying property type A. We can create the corresponding relations: ET1, with primary key A, and ET2, with attribute B. How do we discriminate amongst the tuples in ET2?

Our solution is to insert a reference to ET1 in ET2. Specifically, we add an A attribute in ET2 as a foreign key on the A attribute in ET1. ET2 may have duplicate values for both A and B separately, but each pair will be unique. In other words, the combination of A and B constitutes the key in ET2.

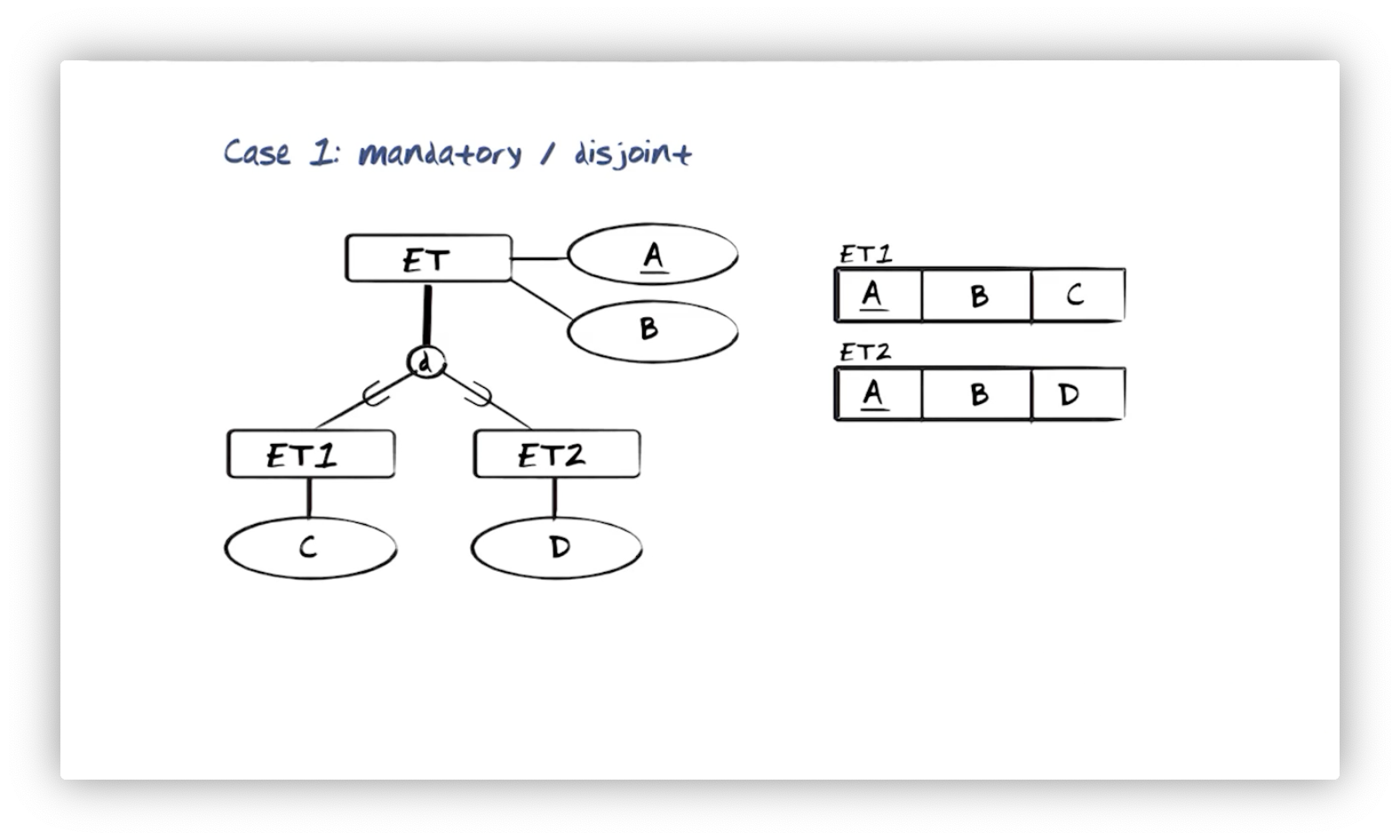
Inheritance: Mandatory Disjoint

Consider three entity types: ET, with identifying property type A and property type B; ET1 with property type C; and ET2, with property type D. ET1 and ET2 are in a mandatory, disjoint, super/subtype relationship with ET, inheriting both A and B from ET. In this relationship, there can be no instances of ET that are neither instances of ET1 nor ET2 (the mandatory constraint), and no instances of ET can be instances of both ET1 and ET2 (the disjoint requirement).

Since the relationship is mandatory, we won't have any concrete instances of ET, so we don't need to create a relation for it. All ET instances will sit as tuples in either the ET1 or ET2 relations. ET1 has primary key A and attributes B and C, and ET2 has primary key A and attributes B and D.

Inheritance: Mandatory, Overlap Allowed

Now consider a mandatory super/subtype relationship between ET and ET1 and ET2, but with overlap allowed. In other words, instances of ET can be instances of ET1 or ET2 or both.

We might represent this system with a single relation, ET, which has a primary key A, attributes B, C, and D, and an attribute named Type. Type holds information indicating whether this tuple is an instance of ET1, ET2, or both.

This option fails for several reasons. Instances of ET1 will always have a NULL value for D, and instances of ET2 will always have a null value for C. Furthermore, we've now coupled the value of the Type attribute to the presence or absence of values for the C and D attributes. We will encounter consistency issues if we update only one and not the other. For example, if we update Type to "Both" but forget to add a value for D, how can we tell if the tuple is an instance of ET1 and ET2, or just ET1?

Let's instead create three relations: ET, with primary key A and attribute B; ET1, with foreign key A on ET and attribute C; and ET2 with foreign key A on ET and attribute D. When we create a new instance of ET, we add a tuple to the ET relation and then to either ET1, ET2, or both.

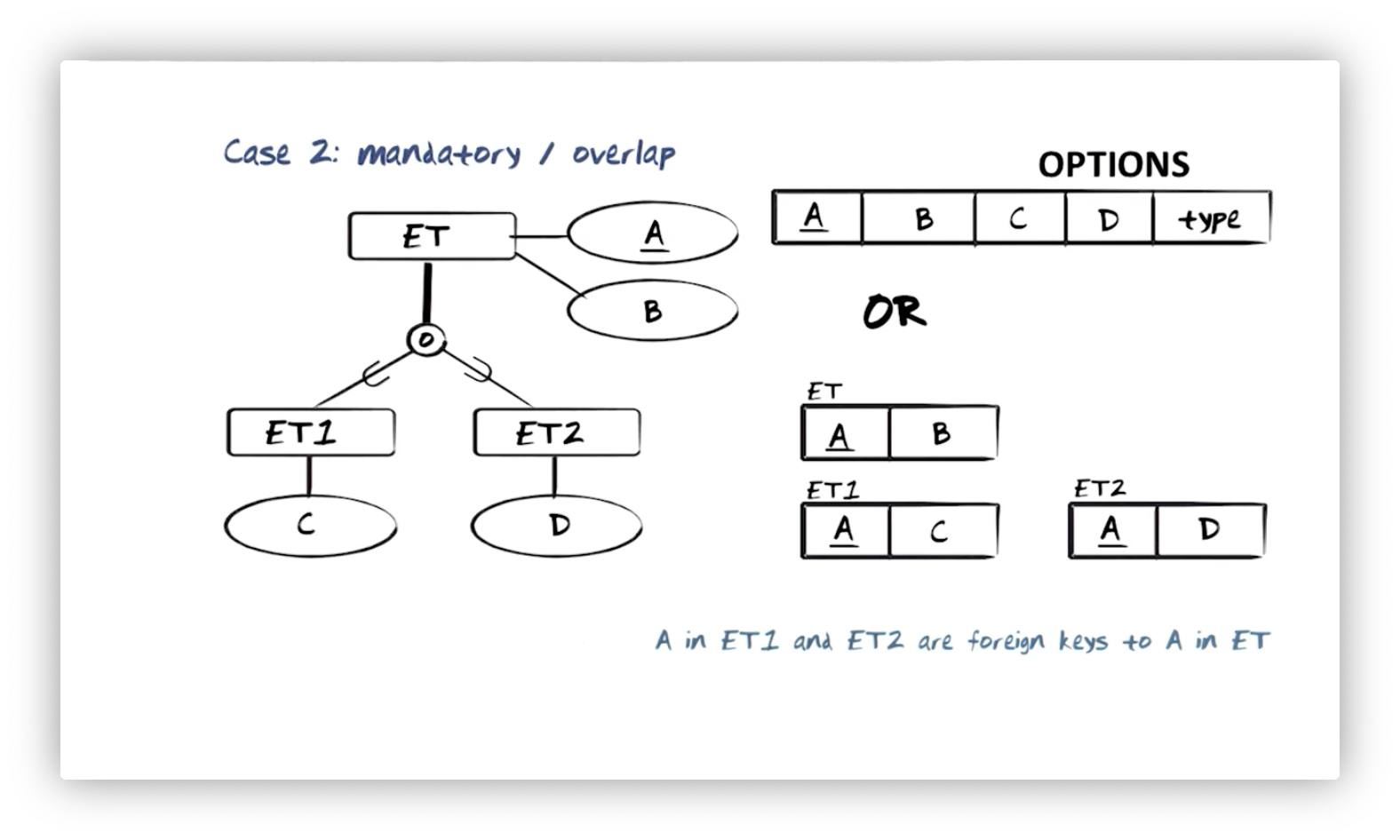
As a minor downside, this solution introduces some redundancy of A values for tuples both in ET1 and ET2. Still, that redundancy is favorable to the excessive NULL values and consistency issues we saw in the other strategy.

Inheritance: Non-Mandatory, Overlap Allowed

Now consider a non-mandatory super/subtype relationship between ET and ET1 and ET2 with overlap allowed. In other words, instances of ET can be instances of ET1, ET2, both, or neither. Again, we can take the Type attribute approach we saw prior, with the added case where both C and D are NULL, but we steer clear of it for the same reasons already discussed.

The solution here is almost identical to that from the previous section. Let's create three relations: ET, with primary key A and attribute B; ET1, with foreign key A on ET and attribute C; and ET2 with foreign key A on ET and attribute D. When creating a new instance of ET, we add a tuple to ET and then either ET1, ET2, both, or neither.

Inheritance: Non-Mandatory, Disjoint

Finally, let's consider the non-mandatory, disjoint relationship type. Again we generate the relations ET, ET1, and ET2, as we saw previously. Since the relationship is not mandatory, we can have tuples in ET not referenced by ET1 or ET2. When references are present, however, the referencing tuple will exist exclusively in ET1 or ET2. As a result, we don't see any of the foreign key redundancy we saw in the overlapping cases.

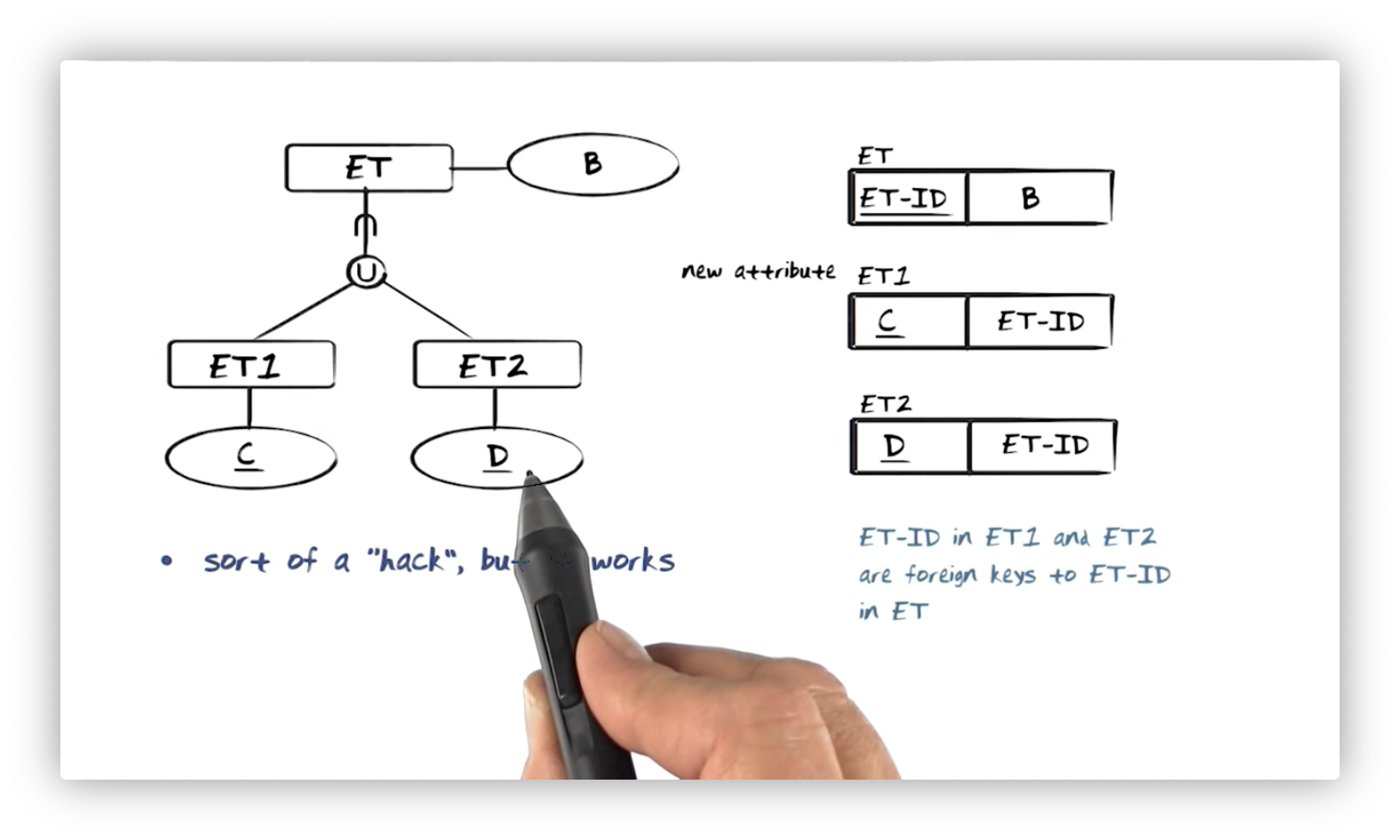
Union Types

Consider an entity type, ET1, with identifying property type C, an entity type, ET2, with identifying property type D, and an entity type, ET, that is the union of ET1 and ET2, with a property type, B. We know that we will have a relation, ET1, with a primary key, C, a relation, ET2, with a primary key, D, and a relation, ET, with attribute B.

We can insert an artificial identifier in the relation ET, ET-ID, which consists of either a value of C or D. Remember, every tuple in ET must be either an instance ET1 or ET2, so we can uniquely identify each tuple by the primary key of one of the union types.